NOTE: The complete notebook of this post is attached at the end.
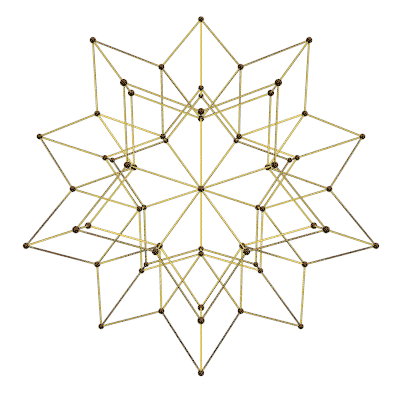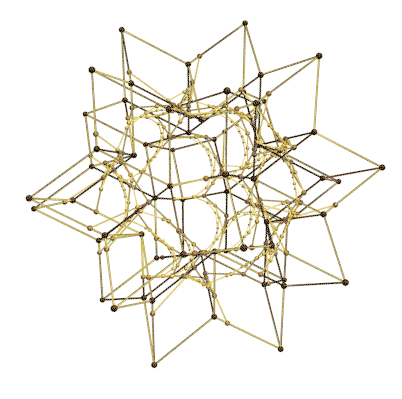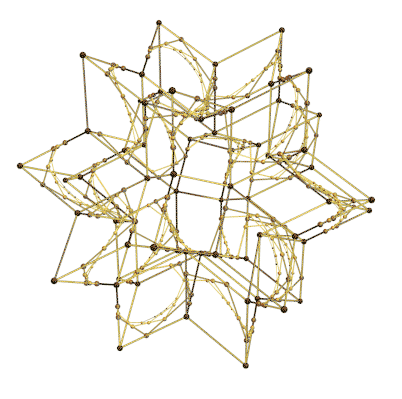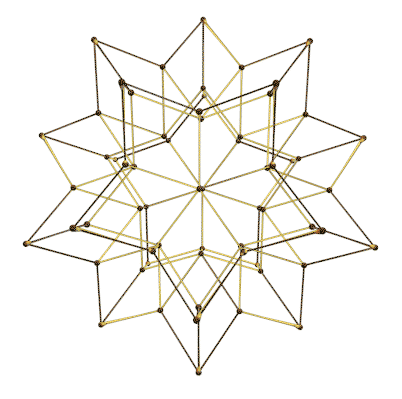
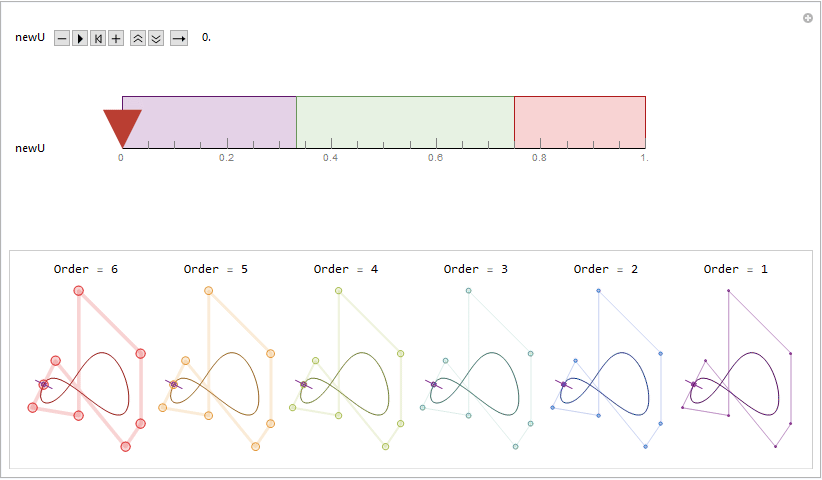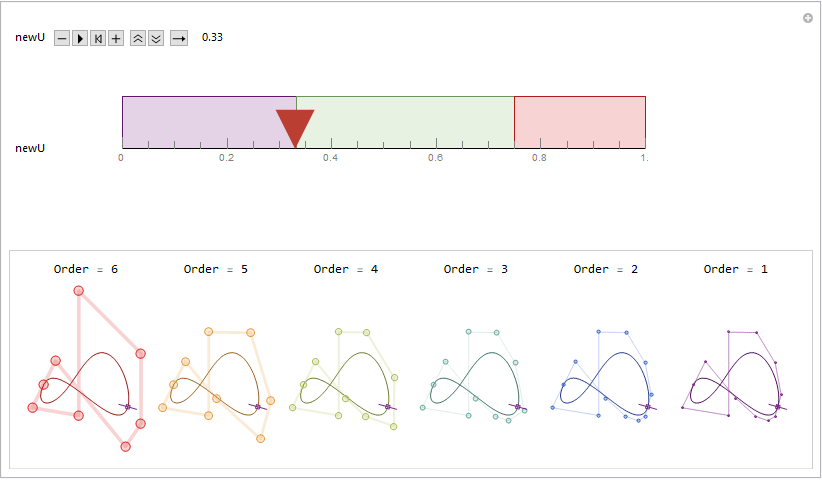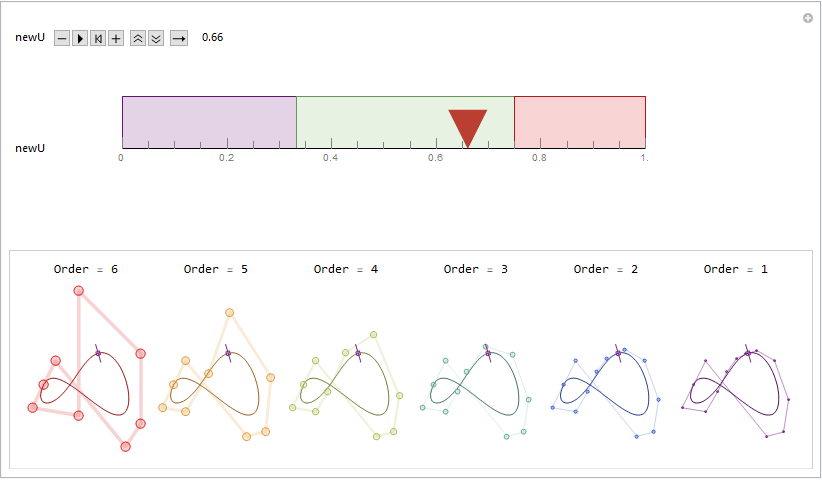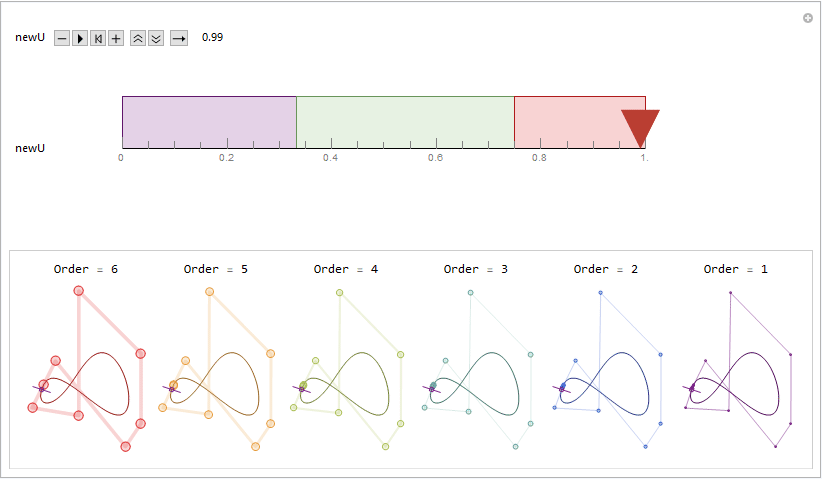
Recently I was reviewing my spline notes. One thing basic yet still attracts me much is the de Boor algorithm. It links the nonlinear, flexible spline curves with nested linear relationships in a rather elegant way.
In the title animation, a repeated knot insertion process is demonstrated. A new knot at position newU is inserted as many times as the degree of the spline. Each diagram with different color represent a refined knot vector along with a refined control point set. By using the built-in B-spline utilities like BSplineCurve and BSplineFunction, each one constructs to the same B-spline curve, with the same parameterization.
It might be more intuitive and visually interesting by stacking those diagrams together. From the stacking result, we can see clearly how each active control points always "sliding" along the edges of their "parent" control polygons. A "LakeColors" scheme is chosen here to give a feeling of blueprint, but it will surely be fun to play with other color schemes by yourself. ;)
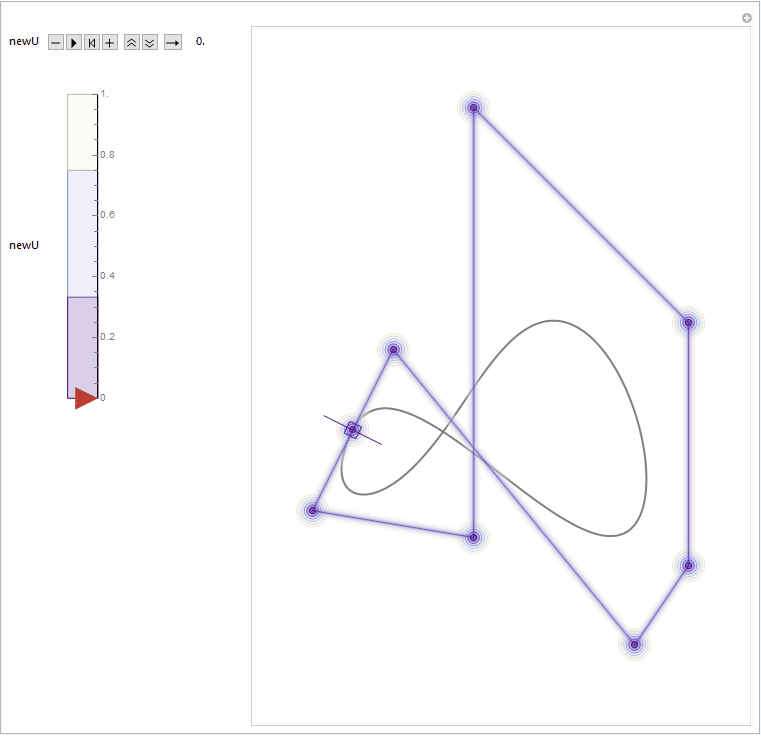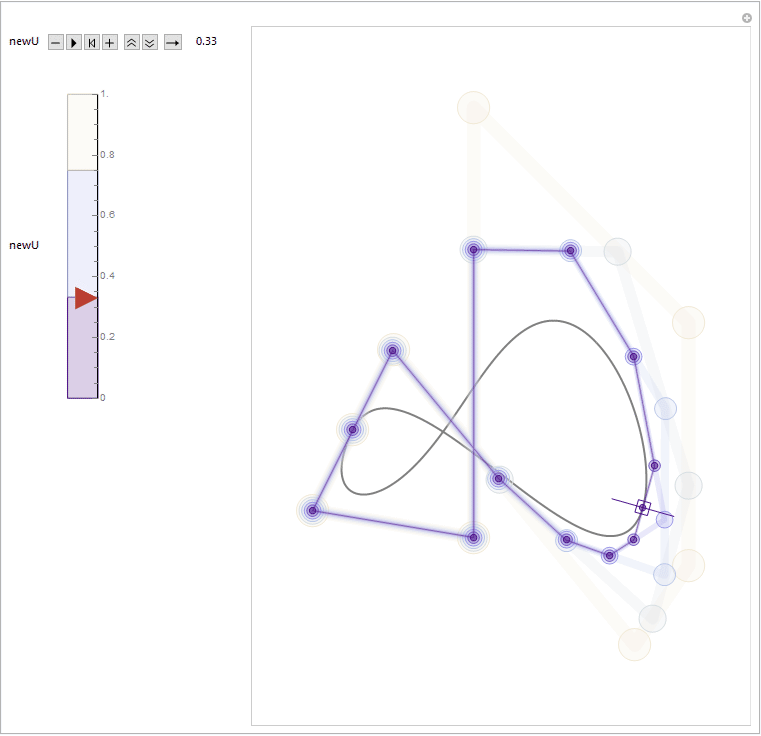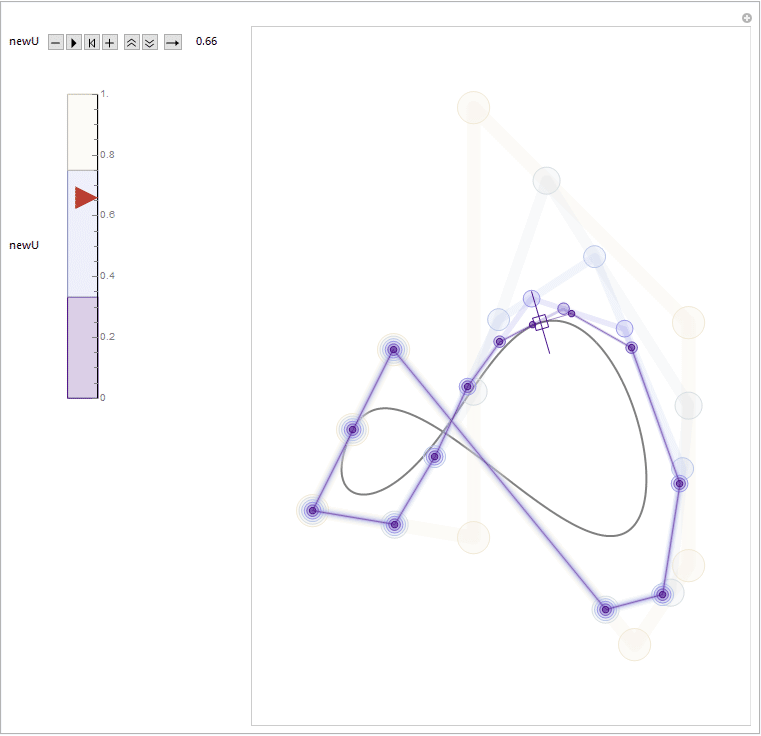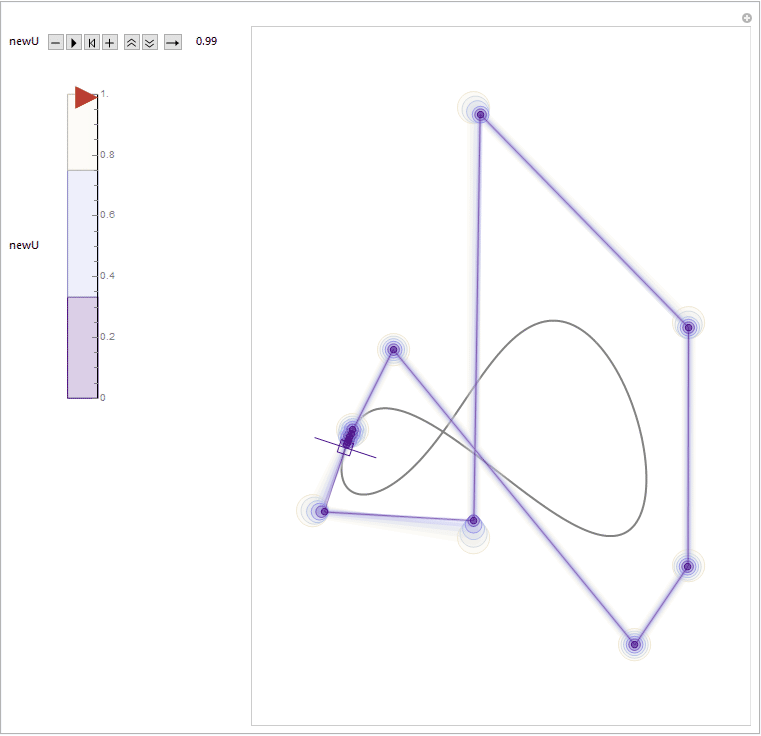
For those who are interested in further exploration, inside the attached notebook (i.e. this one) we have a function splineConfigGen ready for help. It can be used to generate random B-spline configuration and store it to the first argument.
splineConfigGen[myBScfg , <|
"NumCpts" -> 9, "degree" -> 6
, "?radius" -> 2, "?angle" -> 0, "?knot" -> .3
|>]
myBScfg // Function[
{
{GrayLevel[0.7], CapForm[None],
AbsoluteThickness[2],
BSplineCurve[#cpts, SplineKnots -> #knots]
}
, {Hue[0.08333333333333333, 0.4, 1], CapForm[None],
AbsoluteThickness[1],
Line[#cpts]
}
, {FaceForm[GrayLevel[1]], EdgeForm[{Hue[0.08, 1., 1.], Thickness[.005]}],
GeometricTransformation[Disk[{0, 0}, .02],
TranslationTransform /@ #cpts]
}
}
] //
Graphics[{#, GrayLevel[0.8], Circle[{0, 0}, 1]}
, Axes -> True, AxesOrigin -> {0, 0}
, BaseStyle->{BSplineCurveBoxOptions->{Method->{"SplinePoints"->100}}}
] &
The separated and stacked diagrams can be plot easily.
BSAnimationSeperated[ myBScfg ]
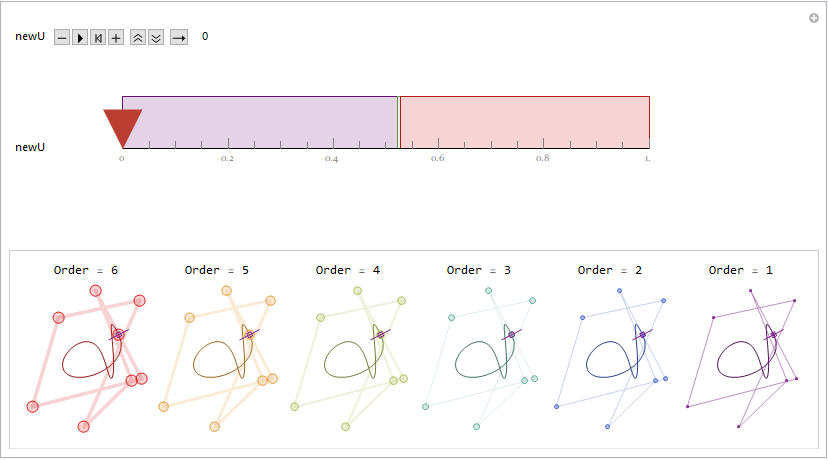
BSAnimationStacked[ myBScfg ]
And one may even discover some nice icon from the found spline.
BSLineArt[ myBScfg ]

Bonus for the new year!
20 knot-insertion processes running on spikey synchronously!

 Attachments:
Attachments: