I'm trying to build an interactive dynamic presentation with
Manipulate about the electric field lines generated by an electric dipole (couple of charges).
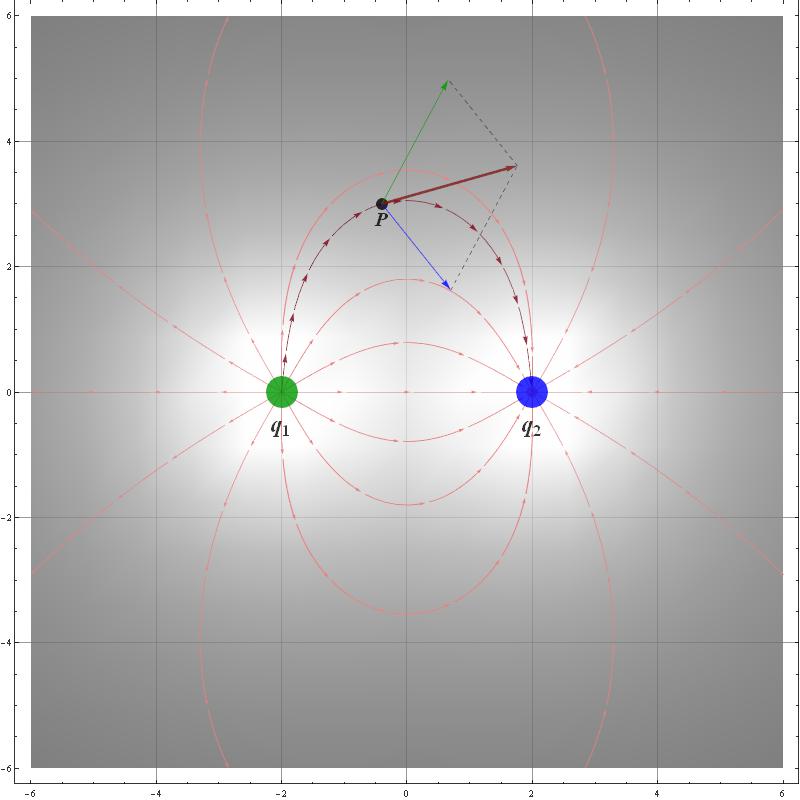
In my plan the user should be able to move the two charges generating the field (through a locator) and there would be a third locator for evaluating the field in that point (say point P). Moreover there will be a specific field line passing through that point P.
I've managed to write the code, but it's
extremely slow.
The problem seems to be that when I move the point P everything is recalculated within the Manipulate expression, even the field lines, that aren't actually affected by the position of the point P and that requires some time machine for Mathematica's end-front to draw the plot (also because the field lines are set to start/end in a specific - user controlled - set of points around the charges).
So how could I let Mathematica know that only some pieces of code must be re-evaluated when interactively moving some single control (i.e. a locator) and other parts need not?
Browsing the documentation I understand that this should be possible, but it's not easy for me to understand the proper command to use (
Hold?
Refresh?) and the structure to give to the Manipulate expression.
So if some expert could give me some advice on how to optimize my code to make the presentation much more responsive to the user's interaction I'd be very grateful.
To be more specific here's the (slow) code I've come up with till now. I understand that changing the position of the charges can be slow, as all the field lines should be recalculated, but simply changing the position of the P point should not be so slow as in this case the other field lines needn't be recalculated.
Manipulate[
DynamicModule[{xPt, yPt, xq1, yq1, xq2, yq2, r, r1, r2, Emag, Emag1,
Emag2, Ex, Ex1, Ex2, Ey, Ey1, Ey2, Exx, Eyy,(*qq1,qq2,*)qf,
VecE, \[Alpha]q, CenterP, FieldPts, EInt}, xPt = startPoint[[1]];
yPt = startPoint[[2]];
xq1 = q1pos[[1]];
yq1 = q1pos[[2]];
xq2 = q2pos[[1]];
yq2 = q2pos[[2]];
(*qq1=SourceCharge1;
qq2=SourceCharge2;*)r1 = N[Sqrt[(xPt - xq1)^2 + (yPt - yq1)^2], 3];
r2 = N[Sqrt[(xPt - xq2)^2 + (yPt - yq2)^2], 3];
Emag1 = qq1/r1^2;
Emag2 = qq2/r2^2;
Ex1 = Emag1*(xPt - xq1)/r1;
Ey1 = Emag1*(yPt - yq1)/r1;
Ex2 = Emag2*(xPt - xq2)/r2;
Ey2 = Emag2*(yPt - yq2)/r2;
Exx = Ex1 + Ex2;
Eyy = Ey1 + Ey2;
VecE[x_, y_] :=
VecE[x, y] = {(qq1 (x - xq1))/((x - xq1)^2 + (y - yq1)^2)^(3/
2) + (qq2 (x - xq2))/((x - xq2)^2 + (y - yq2)^2)^(3/
2), (qq1 (y - yq1))/((x - xq1)^2 + (y - yq1)^2)^(3/
2) + (qq2 (y - yq2))/((x - xq2)^2 + (y - yq2)^2)^(3/2)};
EInt[x_, y_] :=
EInt[x, y] = \[Sqrt](((qq1 (x -
xq1))/((x - xq1)^2 + (y - yq1)^2)^(3/
2) + (qq2 (x - xq2))/((x - xq2)^2 + (y - yq2)^2)^(3/
2))^2 + ((qq1 (y - yq1))/((x - xq1)^2 + (y - yq1)^2)^(3/
2) + (qq2 (y - yq2))/((x - xq2)^2 + (y - yq2)^2)^(3/
2))^2);
\[Alpha]q = ArcTan[(yq2 - yq1)/(xq2 - xq1)];
CenterP = {{(xq1 + xq2)/2, (yq1 + yq2)/2}};
FieldPts =
Flatten[{Table[{xq1 + d Cos[\[Alpha] + \[Alpha]q],
yq1 + d Sin[\[Alpha] + \[Alpha]q]}, {\[Alpha], 0,
2 \[Pi], \[Pi]/(3 2^s)}],
Table[{xq2 + d Cos[\[Alpha] + \[Alpha]q],
yq2 + d Sin[\[Alpha] + \[Alpha]q]}, {\[Alpha], 0,
2 \[Pi], \[Pi]/(3 2^s) If[qq2 == 0, 2 3 2^s,
Min[2 \[Pi], Abs[qq1]/Abs[qq2]]]}]}, 1];
Show[{DensityPlot[
0.1 + (2/\[Pi] ArcTan[EInt[x, y]])^ExCol, {x, -6 + offset,
6 - offset}, {y, -6 + offset, 6 - offset},
ColorFunction -> GrayLevel, ColorFunctionScaling -> False,
ImageSize -> 800, GridLines -> Automatic,
BaseStyle -> Directive[Opacity[0.8]],
Epilog -> {Text[Style[P, 20, RGBColor[0, 0, 0], Bold, Italic],
startPoint, {0, 1.5}],
Text[Style[Subscript[q, 1], 24, RGBColor[0, 0, 0], Bold],
q1pos, {0, 2.5}],
Text[Style[Subscript[q, 2], 24, RGBColor[0, 0, 0], Bold],
q2pos, {0, 2.5}],
Arrowheads[.015], {Dashed, GrayLevel[0.25],
Line[{{VS*Ex2 + xPt, VS*Ey2 + yPt}, {VS*Exx + xPt,
VS*Eyy + yPt}}]}, {Dashed, GrayLevel[0.25],
Line[{{VS*Exx + xPt, VS*Eyy + yPt}, {VS*Ex1 + xPt,
VS*Ey1 + yPt}}]}, {RGBColor[0, 0.6, 0],
Disk[q1pos, .25]}, {Blue, Disk[q2pos, .25]}, {Black,
Disk[startPoint, .1]}, {Thin, RGBColor[0, 0.6, 0],
Arrow[{startPoint, {VS*Ex1 + xPt, VS*Ey1 + yPt}}]}, {Thin,
Blue, Arrow[{startPoint, {VS*Ex2 + xPt,
VS*Ey2 + yPt}}]}, {Thickness[0.0035],
RGBColor[0.5, 0.1, 0.1],
Arrow[{startPoint, {VS*Exx + xPt, VS*Eyy + yPt}}]}}],
If[field,
StreamPlot[
VecE[x, y], {x, -6 + offset, 6 - offset}, {y, -6 + offset,
6 - offset},
StreamPoints -> {{FieldPts ->
Directive[Thickness[Tiny], RGBColor[0.9, 0.5, 0.5]], 1},
Fine, Scaled[1]}, StreamScale -> {0.08, 0.1, 0.0055},
ImageSize -> 800],
StreamPlot[{0, 0}, {x, -6 + offset, 6 - offset}, {y, -6 + offset,
6 - offset}, StreamPoints -> None,
StreamScale -> {0.08, 0.1, 0.0055}]],
StreamPlot[
VecE[x, y], {x, -6 + offset, 6 - offset}, {y, -6 + offset,
6 - offset},
StreamPoints -> {{{startPoint, RGBColor[0.5, 0.0, 0.1]}}},
StreamScale -> 0.05, ImageSize -> 800, GridLines -> Automatic](*,
StreamScale\[Rule]0.06*)}]], {{startPoint, {-0.4,
3}}, {-7, -7}, {7, 7},
Locator}, {{q1pos, {-2, 0}}, {-7, -7}, {7, 7},
Locator}, {{q2pos, {2, 0}}, {-7, -7}, {7, 7}, Locator},
Grid[{{Control[{{qq1, 2, "\!\(\*SubscriptBox[\(q\), \(1\)]\)"}, -4,
4, .5, Appearance -> "Labeled"}],
Control[{{qq2, -2, "\!\(\*SubscriptBox[\(q\), \(2\)]\)"}, -4,
4, .5, Appearance -> "Labeled"}]}, {Control[{{d, 0.7,
"lines start distance form charges"}, 0.1, 4, 0.1,
Appearance -> "Labeled"}],
Control[{{s, 1, "lines density"}, 1, 4, 1,
Appearance -> "Labeled"}]}, {Control[{{VS, 13, "Vector Scale"},
0, 25, 1, Appearance -> "Labeled"}],
Control[{{ExCol, 0.3, "Color Scale"}, 0, 1, 0.2,
Appearance -> "Labeled"}]}, {Control[{{offset, 0,
"Global range"}, -4, 4, 0.5, Appearance -> "Labeled"}],
Control[{{field, True, "Show Field lines"}, Checkbox}]}},
Frame -> All], ControlPlacement -> Top]
Actually, if the code regarding the definition of the field lines starting points:
FieldPts =
Flatten[{Table[{xq1 + d Cos[\[Alpha] + \[Alpha]q],
yq1 + d Sin[\[Alpha] + \[Alpha]q]}, {\[Alpha], 0,
2 \[Pi], \[Pi]/(3 2^s)}],
Table[{xq2 + d Cos[\[Alpha] + \[Alpha]q],
yq2 + d Sin[\[Alpha] + \[Alpha]q]}, {\[Alpha], 0,
2 \[Pi], \[Pi]/(3 2^s) If[qq2 == 0, 2 3 2^s,
Min[2 \[Pi], Abs[qq1]/Abs[qq2]]]}]}, 1];
is commented out, the presentation becomes much more quick (but the plot will show just the single field lines passing through the point P).
Here is a static image of my WIP presentation: