Open code in Cloud | Download code to Desktop via Attachments Below
Inspired by Peano Surface example and the phenomenal British children TV series Peppa Pig. According to the linked report, the series
has swept China and garnered fans of all ages

Usually Peppa the protagonist lives in her peaceful 2-D village in Euclidean space. Lets relocate her for a moment to a smooth manifold where Riemann distance is well defined in case she needs to walk around. In this case, the new smooth surface is a Möbius band.
*Right click to download Peppa's image:



Pay close attention to the unusual rotation pattern at end of the strip far away and on the left side. Comparing to the rotation pattern on a non-twisted cylinder shell, which is a very trivial case:


The second argument v in the parametric form for a Möbius band in Mathematica determines the starting point for the band. If you continuously increase v from a initial value, you can animate the flow of Peppa Pig on the band:


The nose direction of the avatar (inward vs outward pointing) flips as it flow pass the twisting mark.
Further step is about a classic question: what will happen if we
cut a Möbius strip down the middle
well this answer is not intuitive until we ask Wendy Wolf for help. Let me show you the cute screenshot code first, filled with adorable animation figures.
*Right click to download Wendy's image:



If you observe the band with two characters closely, you will find something useful. Imagine that you have a pair of scissors to cut along the middle seam. You can tell that the dash line is ALWAYS, in the middle of Peppa's nose-tip and Wendy's neck, regardless of number of twists.

Well just by look at the joint of this Möbius band, you may have the conclusions:
- Two Peppa's: looking left and right
- Two Wendy's: looking left and right
Also you may observe that
- whenever we have a switch between Peppa and Wendy, their facing direction flips, either left to right or vice versa
But as you draw Peppa and Wendy on a letter paper (orientable), you won't be able to find a valid arrangement to meet the requirements above at the same time:
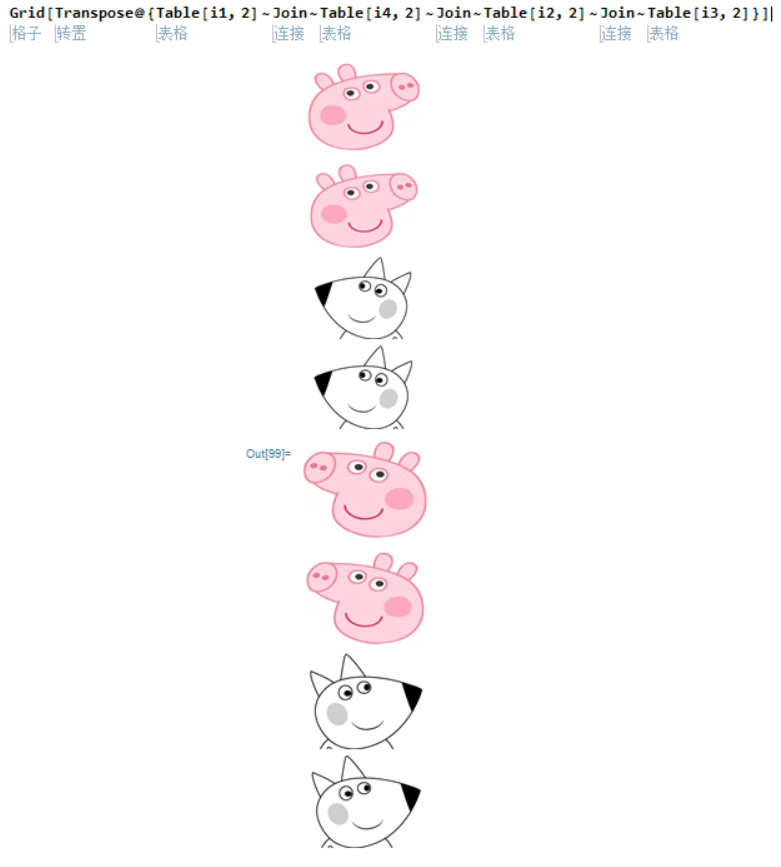
What happened? Non-orientability takes affect. Usually people talking about Möbius, they are talking about flipping in and out. In fact, up/down and left/right are no longer defined after half twist!
The rules the arrangement should follow are that
- the middle line is in between Peppa's nose and Wendy's neck. The middle line is by nature immune to the twist operation.
- face direction alternation, which is introduced by the twist operation
- annihilation of the distinction of left and right
You can derive the argument above naturally by asking how you have learned to define the direction of a plane in school? take out your right hand to thumb up, then curl the four fingers inward with curled pinky finger laying on a chosen side of the plane. Since the surface is no longer orientable, curling direction does not matter any more. Neither does the left and right distinction.
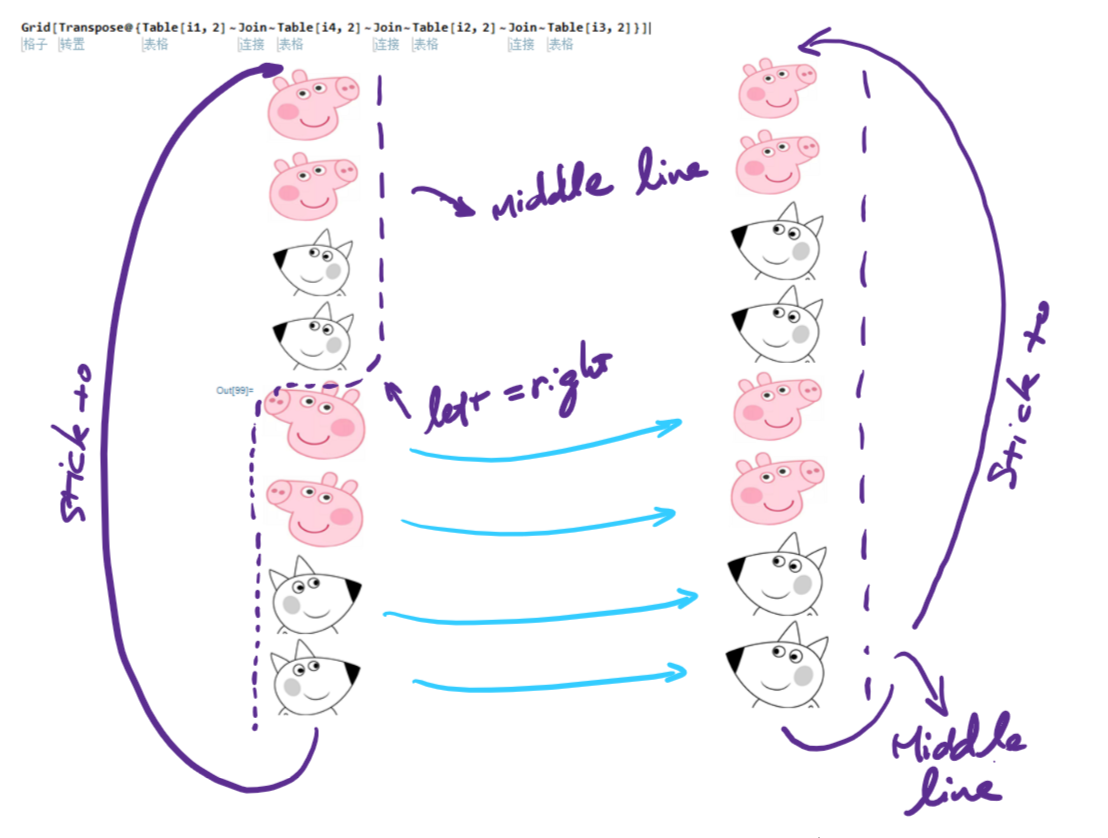
As illustrated above, we know there is one half-twist every time we count 4 (2 Peppa and 2 Wendy). We already have one in the middle of the column. At the bottom where Wendy is joined with Peppa on the top, we have one more half-twist because the glue line is exactly 4 items away from the first one. And two half-twists give us a full twist!
So go back to the question above: What do we have if a Möbius band is cut down the middle? Answer is another Möbius band with double the length and a full twist!
After all this fun, because mapping from Möbius band to a planar square is bijective, we can dismiss Peppa and her friends and return them to their happy land. Let them enjoy the family reunion and sunshine on the yard.
 Attachments:
Attachments: