MODERATOR NOTE: a submission to computations art contest, see more: https://wolfr.am/CompArt-22
Open Code in Cloud | Download Code to Desktop via Attachments Below
Mirror anamorphism is effectively: "what you get is NOT what you see". Unless you have the right mirror at hand! Some time ago, in my previous Wolfram Demonstrations Cylindrical Mirror Anamorphosis and Cylindrical Anamorphosis of Some Popular Images, I showed how geometric figures or line drawings could be converted to static anamorphic images. To see the Bugs Bunny figure below, you need a cylindrical mirror to see the correct image.  The same function as in those demonstrations (cylindricalAnamorphMapCF), that maps image points inside the mirror to their corresponding anamorphic coordinates, can be used to create moving images. This is the way to create an "anamorphic movie". These are the Graphics primitives used: points along the edges of polygons or rose curves.
The same function as in those demonstrations (cylindricalAnamorphMapCF), that maps image points inside the mirror to their corresponding anamorphic coordinates, can be used to create moving images. This is the way to create an "anamorphic movie". These are the Graphics primitives used: points along the edges of polygons or rose curves.
polygonPoints[\[Theta]0_,r_,n_,m_:51]:=Table[{0,.75}+r Cos[Pi/n]Sec[(2ArcTan[Cot[(1/2)n(\[Theta]-\[Theta]0)]])/n]{Cos[\[Theta]],Sin[\[Theta]]},{\[Theta],0,2\[Pi],\[Pi]/m}]
rosePoints[\[Theta]0_,r_,n_,m_:51]:=1/3Table[{0,2.25}+r{(Sin[n \[Theta]+\[Theta]0]+2) Cos[ \[Theta]],Sin[ \[Theta]] (Sin[n \[Theta]+\[Theta]0]+2)},{\[Theta],0,2\[Pi],\[Pi]/m}]
colors={RGBColor[0.965, 0.3285, 0.0785],RGBColor[0.266, 0.516, 0.9576],RGBColor[0.207, 0.652, 0.324],RGBColor[0.988, 0.73, 0.0195]};
The first step is to generate a series of frames to get a moving image. Here we use a rotating square.
frames = Table[Module[{n = 4, r = 1., ptsC, ptsP, ptsS, m = 55},
ptsC = CirclePoints[{0, .75}, r, m];
ptsP = polygonPoints[\[Theta]0, r, n, m];
ptsS = polygonPoints[\[Pi]/4., 1.425 r, 4, 2 m];
Graphics[{EdgeForm[Thick], FaceForm[cols[[2]]], Polygon[ptsS],
FaceForm[cols[[3]]], Polygon[ptsC], FaceForm[cols[[1]]],
Polygon[ptsP]}, ImageSize -> 275]],
{\[Theta]0, 0.05, 6.3, 6.3/51}];
ListAnimate[frames]
Next we make an anamorphic map of each frame:
anamorphFrames =
frames /. {x_?NumericQ, y_?NumericQ} ->
cylindricalAnamorphMapCF[{x, y}, {7., 5}] // Quiet;
ListAnimate[anamorphFrames]
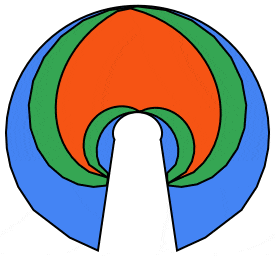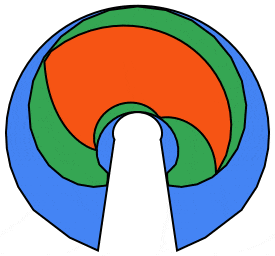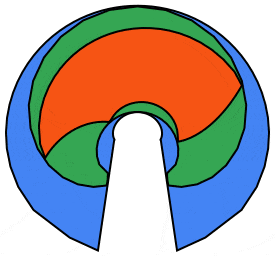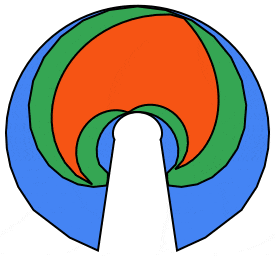
We can do better using the 5 petaled rose curve:
frames = Table[Module[{n = 5, r = 1., ptsC, ptsP, ptsS, m = 55},
ptsC = CirclePoints[{0, .75}, r, m];
ptsCc = CirclePoints[{0, .75}, .32 r, m];
ptsP = rosePoints[\[Theta]0, r, n, m];
ptsS = polygonPoints[\[Pi]/4., 1.425 r, 4, 2 m];
Graphics[{EdgeForm[Thick], FaceForm[cols[[2]]], Polygon[ptsS],
FaceForm[cols[[4]]], Polygon[ptsC], FaceForm[cols[[3]]],
Polygon[ptsP], FaceForm[cols[[1]]], Polygon[ptsCc]},
ImageSize -> 275]],
{\[Theta]0, 0.05, 6.3, 6.3/51}];
anamorphFrames =
frames /. {x_?NumericQ, y_?NumericQ} ->
cylindricalAnamorphMapCF[{x, y}, {7., 5}] // Quiet;
duoFrames = Row /@ Transpose[{frames, anamorphFrames}];
ListAnimate[duoFrames]
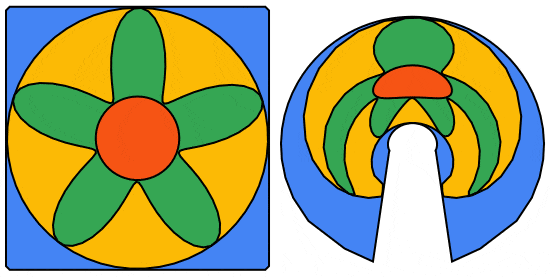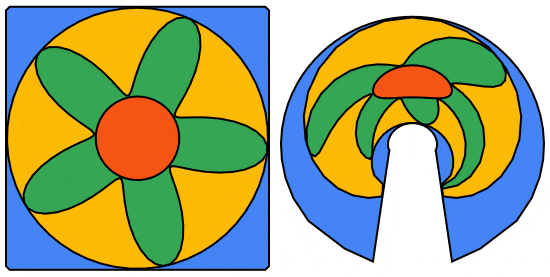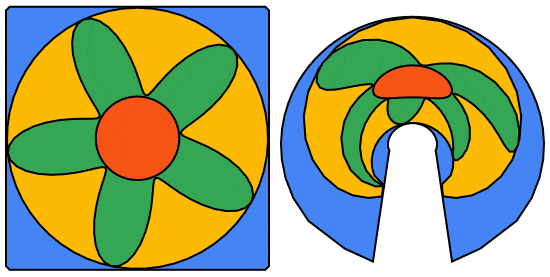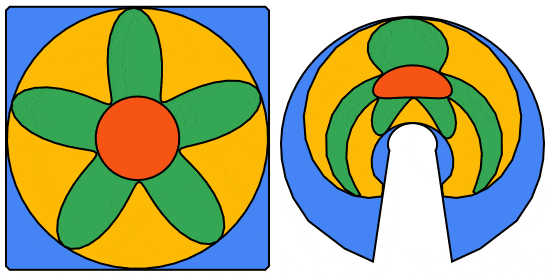
Now, we convert the anamorphFrames list to a GIF using Export (file attached).
Export["rose5.gif", Most@anamorphFrames]
We can subsequently transfer the GIF to an iPad (e.g. via AirDrop). We let the GIF run on the iPad and put a fitting cylindrical mirror on top. I used reflective window foil rolled over a cardboard tube. And we set up our camera to take an MP4 or MOV movie.

This is how the movie looks like (converted to GIF for use in the Community editor).

This is a small scale experiment using an iPad. But an iPadPro, any flat screen TV monitor or array of monitors could be used. This could be combined by working with much more sophisticated images or even photographs. Imagine a floor with an array of n x m LCD monitors, a vertical mirror column in the middle. Unrecognizable images floating on the floor while people walk around admiring the real movie reflected inside the cylindrical mirror column! Way beyond my means but maybe an idea for Wolfram Language inspired artists or architects?
 Attachments:
Attachments: