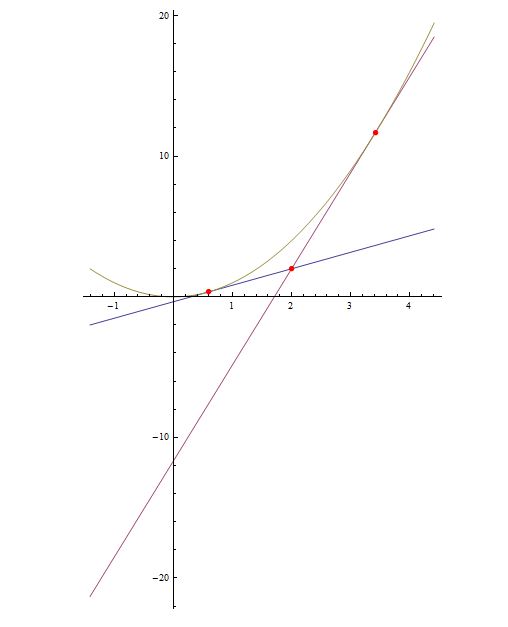
Just a little code to show the 2 tangents in question. Have made a slight change to the code to account for negative co-ordinate points, and it will only only account for quadratics, things are very unpredictable if higher powers are used.
Clear[x, y, f]; p = {2, 2}; f[x_] := x^2 ;
dif = D[f[x], x];
pts = Solve[f[x] - p[[2]] == dif (x - p[[1]]), x];
pts = x /. pts;
t1 = Simplify[f[pts[[1]]]];
t2 = Simplify[f[pts[[2]]]];
m1 = (p[[2]] - t1)/(p[[1]] - pts[[1]]); m2 = (p[[2]] - t2)/(
p[[1]] - pts[[2]]);
Plot[{m1 (x - pts[[1]]) + t1, m2 (x - pts[[2]]) + t2, f[x]}, {x,
pts[[1]] - 5, pts[[2]] + 4},
Epilog -> {PointSize[0.015], Red, Point[{p[[1]], p[[2]]}],
Point[{pts[[1]], t1}], Point[{pts[[2]], t2}]}, AspectRatio -> 5/3,
ImageSize -> {600, 600}]