Please download the notebook at the end of the discussion

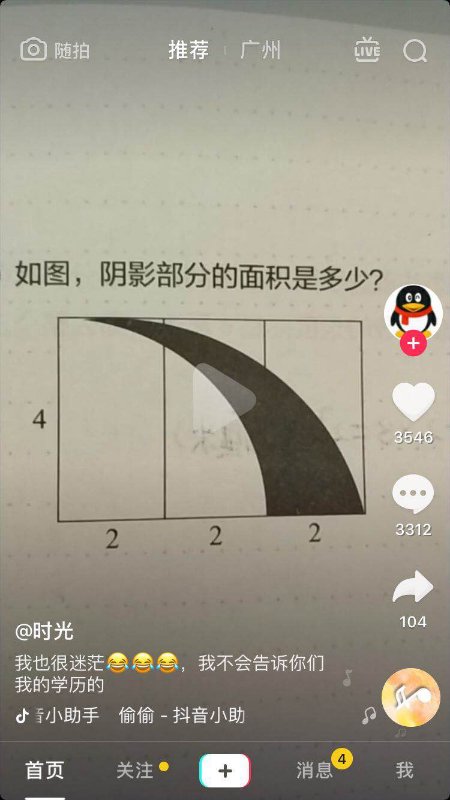
This is a problem posted by a TikTok user. The origional version is for middle school students, so it is safe to assume the two arcs in the problem are from two separated circles. They are tangent to each other at the left top corner of the given rectangle.

Let's extend this problem to a more general case if the longer arc is part of conic section. We can give the coordinates to some points in the picture: $(0,0)$, $(2,0)$,$(4,0) $,$(6,0)$, where the origin is at the left bottom corner.

Clear["Global`*"]
longArc[x_, y_] := x^2/a^2 + (y + h)^2/(h + 4)^2

longArc is the implicit form of an ellipse of which the two axes are parallel to x and y axis respectively. The center of the ellipse is said to move downward along the y axis. So the coordinate of the center of ellipse is $(0, -h)$. The semi minor axis in y direction is $b = h+4$. We denote a for the semi-major axis. Solve for a in terms of h:

Reduce[36/a^2+h^2/(4+h)^2==1&&h>0&&a>0,{a}]

we have

h>0&&a==(3 Sqrt[(16+8 h+h^2)/(2+h)])/Sqrt[2]

Now we can define eccentricity of the ellipse as

ecc[h_]:=With[{a=(3 Sqrt[(16+8 h+h^2)/(2+h)])/Sqrt[2]},Sqrt@Abs[a^2-(h+4)^2]/Max[a,h+4]] 

in case there is a switch. Use Manipulate function to verify the set of valid ellipses:

Manipulate[
 a = (3 Sqrt[(16 + 8 h + h^2)/(2 + h)])/Sqrt[2];
 GraphicsRow@{ContourPlot[{x^2/a^2 + (y + h)^2/(h + 4)^2 == 1, 
     x^2 + y^2 == 16}, {x, -10, 10}, {y, -10, 10}, 
    Epilog -> {Point[{6, 0}], Line[{{0, 4}, {6, 4}, {6, 0}}]}, 
    Axes -> True],
   Plot[ecc[t], {t, 0, 8}, PlotLabel -> "Eccentricity", 
    Epilog -> {PointSize[0.03], Point[{h, ecc[h]}]}]
   }, {h, 0, 8}]

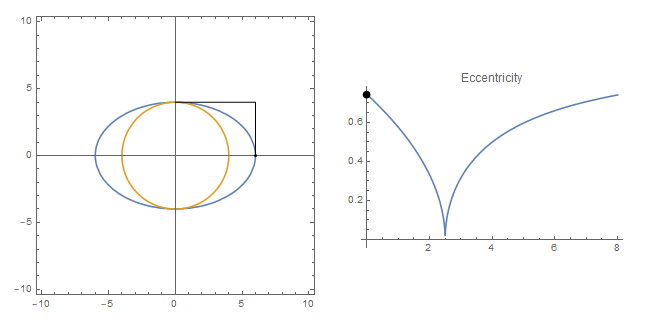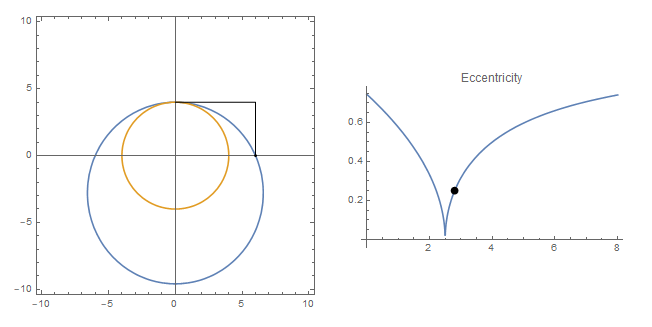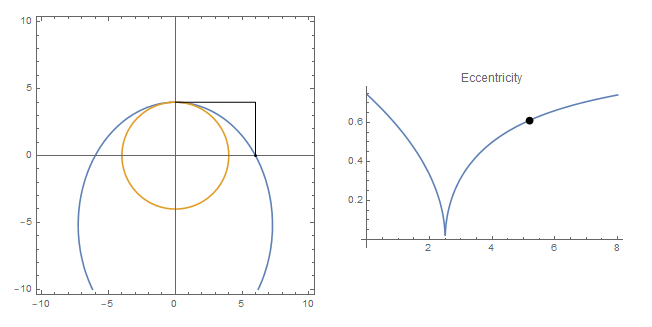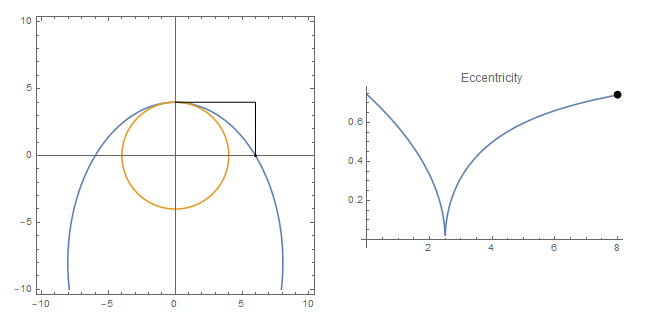
Note that if the eccentrity is zero (downward cusp), we have the a circle that is to be found in the original question.

Discussion

• If h is negative, as the center of ellipse move upward, the ellipse will intersect with the vertical line on the right twice:

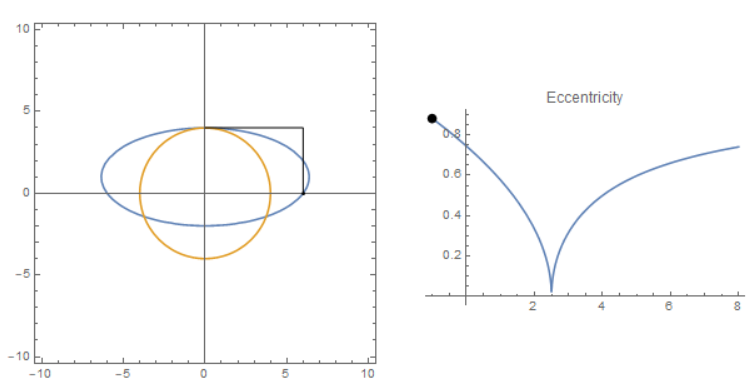
• If h approaches positive infinite, as the ellipse is stretched very long downward, there exists a limit:

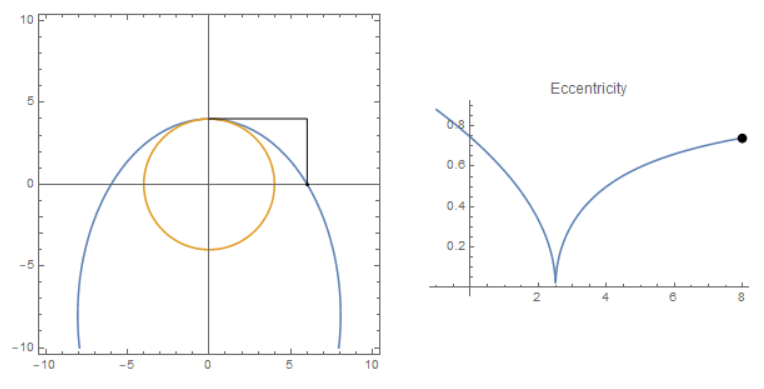
Because h is very large, the eccentricity is very close to 1 according to the graph on the right side. Thus the limit of the streched ellipse is a parabola, with vertex at $(4,0)$ and facing downward. The closed form expression is:

y - 4 =  -1/9 x^2

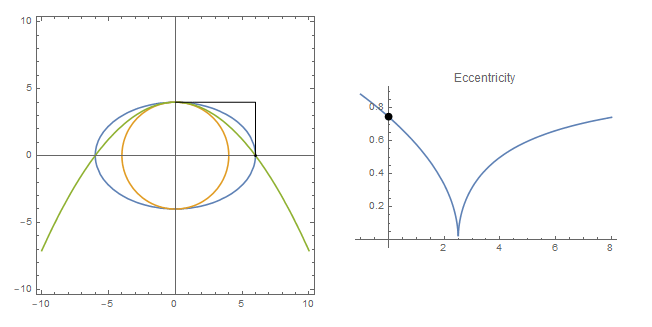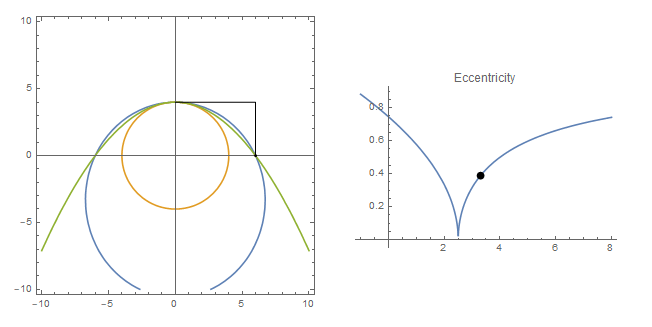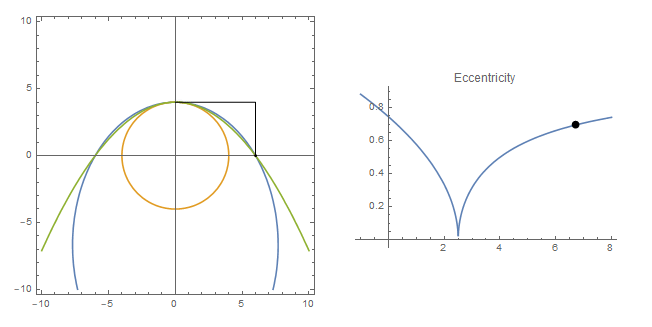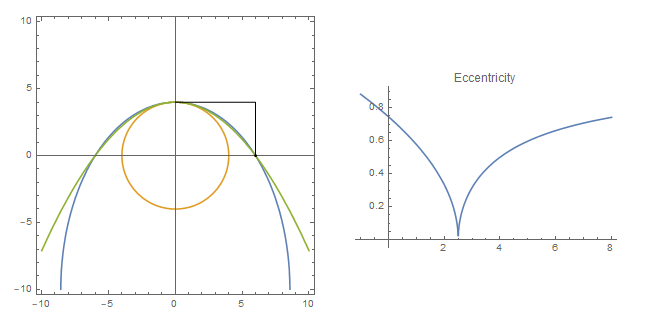
Use the following plot function in the Manipulate function above to see the animation with three curves in one plot:

ContourPlot[
 {
  x^2/a^2 + (y + h)^2/(h + 4)^2 == 1,
  x^2 + y^2 == 16,
  9*(y - 4) == -x^2
  }, {x, -10, 10}, {y, -10, 10}...]

Find Numeric Area

ImplicitRegion is used in a very straight forward manner. Given h is 4:

Module[{h=4,a},
a=(3 Sqrt[(16+8 h+h^2)/(2+h)])/Sqrt[2];
\[ScriptCapitalR]=ImplicitRegion[x^2+y^2> 16&&x^2/a^2+(y+h)^2/(h+4)^2< 1&&x>0&&y>0,{x,y}];
DiscretizeRegion[\[ScriptCapitalR]]
]

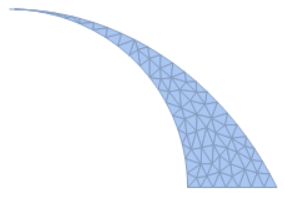
Compute the area of the region by:

Area[%]
=> 4.45849

Attachments:

ellipse.nb