To celebrate the upcoming Pi day, wouldn't it be nice to find your name within the digits of Pi? This, along with the entire works of William Shakespeare, allegedly also present there! Let's try it with Mathematica! This is an estimate of our chances for finding a word or name of a certain length within the first 100 million digits of Pi:
Grid@Import["http://www.angio.net/pi/whynotpi.html", "Data"][[-1, 1]]

Although you can find up to 5 trillion (! ) digits of Pi on the web, I limit myself here to using the Mathematica commands Pi and RealDigits. Let's first convert Pi to base 26 and map the digits 0-25 to the characters A-Z.
piDigits26Window[startPosition_, width_] :=
FromCharacterCode /@ (First@
RealDigits[Pi, 26, width, -startPosition + 1] + 65)
Using this function, this Manipulate is an "Alphanumerical Pi-Inspector" and opens a window along the first 1 million characters in the base 26 expansion of Pi.
Manipulate[
Row[{Row@piDigits26Window[i - 6, n],
Framed[Style[StringJoin @@ piDigits26Window[i, n], 18, Bold]],
Row@piDigits26Window[i + n, n]}], {{i, 7, "starting position",
ImageSize -> Small}, 7, 1000000, 1}, {{n, 7, "window width"},
Range[10]}]
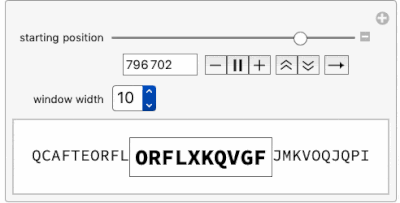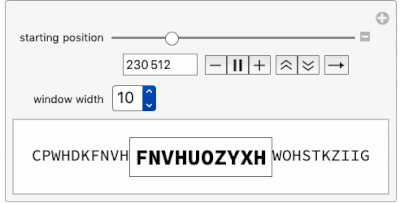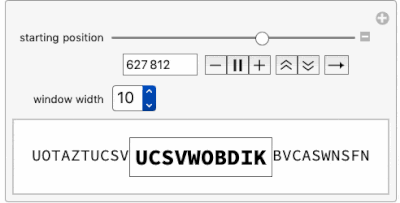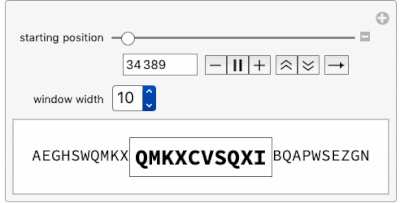
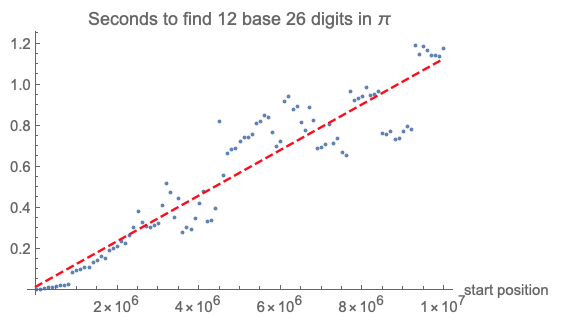
Moving the "starting position" slider toward 1 million already shows a certain delay and proves that going into millions of digits may be time consuming. Let's look at the time needed to find 12 consecutive base 26 digits within Pi:
timeToFind[start_] := RepeatedTiming@piDigits26Window[i, 12]
times = ParallelTable[{i, timeToFind[i] // First}, {i, 1, 10000001,
100000}];
fit = FindFit[times, a x + b, {a, b}, x];
Show[
ListPlot[times,
PlotLabel -> "Seconds to find 12 base 26 digits in \[Pi]",
AxesLabel -> {"start position", None}],
Plot[a x + b /. fit, {x, 0, 10000000},
PlotStyle -> Directive[Dashed, Red]]]
Let's see things at a smaller scale and try to find any (and who knows our?) name within the digits of Pi. Here is a list of 2007 popular names from the internet:
data = Import["https://nameberry.com/popular_names/US", "Data"];
allNames = Most@Cases[Rest[data[[-2, 2, 1]]], _?StringQ, \[Infinity]];
And a function to extract names of a certain length from this list:
nLetterNames[n_] :=
ToUpperCase /@ Cases[allNames, _?(StringLength[#] == n &)]
nLetterNames[10]

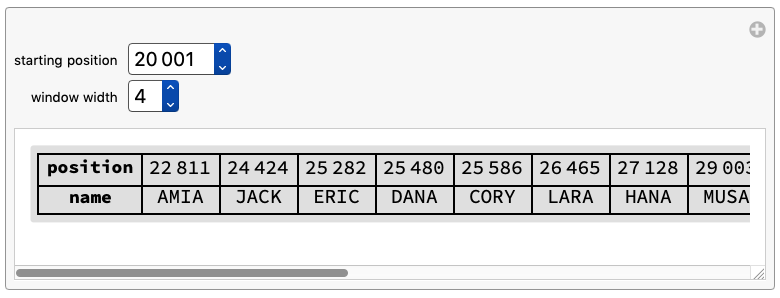
You can use this Manipulate to find maybe your name. Mine is at position 25282 (unfortunately with a C i.o a K!)
Manipulate[(*for the first 100,000 digits of base 26 Pi*)
Module[{windowStrings, names, matches, positions},
names = nLetterNames[n];
windowStrings =
Table[StringJoin @@ piDigits26Window[i, n], {i, start,
start + 20000}];
matches = Flatten[ParallelMap[Cases[names, #] &, windowStrings]];
positions = Position[windowStrings, #] + start - 1 & /@ matches;
Highlighted[
Grid[{Grid /@ Join[{{{Style["position", Bold, 12]}}}, positions],
Join[{Style["name", Bold, 12]}, matches]}, ItemSize -> Full,
Frame -> All], Background -> Lighter[Gray, 0.75]]],
{{start, 20001, "starting position"}, Range[1, 100001, 20000]},
{{n, 4, "window width"}, Range[2, 7]}, SynchronousUpdating -> False,
ContentSize -> {500, 100}]
ZARA appears twice: at positions 39922 and 678268
Row[{piDigits26Window[39922, 4], piDigits26Window[46796, 4]}]
And so does CLYDE at 233074 and 700576
Row[{piDigits26Window[233074, 5], piDigits26Window[700576, 5]}]
If you cannot find your name in Pi, maybe it is hidden in the Champernowne number? This is a "normal" number where all digits appear with equal frequency. Pi is only conjectured to be normal and so your chances of finding any name are higher with Champernowne? Next, the adapted Manipulate with Pi replaced by Champernowne[]:
cbDigits26Window[startPosition_, width_] :=
FromCharacterCode /@ (First[
RealDigits[ChampernowneNumber[], 26,
width, -startPosition + 1]] + 65)
Manipulate[(*for the first 100,000 digits of the base 26 Champernowne \
number*)
Module[{windowStrings, names, matches, positions},
names = nLetterNames[n];
windowStrings =
Table[StringJoin @@ cbDigits26Window[i, n], {i, start,
start + 20000}];
matches = Flatten[ParallelMap[Cases[names, #] &, windowStrings]];
positions = Position[windowStrings, #] + start - 1 & /@ matches;
Highlighted[
Grid[{Grid /@ Join[{{{Style["position", Bold, 12]}}}, positions],
Join[{Style["name", Bold, 12]}, matches]}, ItemSize -> Full,
Frame -> All], Background -> Lighter[Gray, 0.75]]],
{{start, 1, "starting position"}, Range[1, 100001, 20000]},
{{n, 4, "window width"}, Range[2, 7]}, SynchronousUpdating -> False,
ContentSize -> {500, 100}]

Good Luck! And share your findings before 3-14...