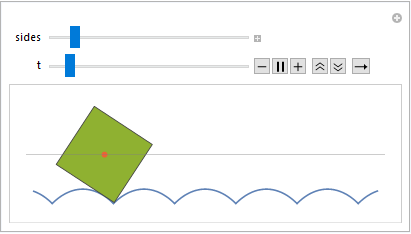
By this time, people are already familiar with Stan Wagon's demonstration of rolling regular polygons over a piecewise catenary road, as first shown in his paper with Leon Hall.
The purpose of this post is to show a particularly compact Manipulate[] demonstration for rolling regular polygons, as well as a variation where the wheel is a Reuleaux polygon.
This hinges on two things: NDSolve[]'s ability to cope with discontinuous differential equations, and the existence of a usable polar equation in both the regular and Reuleaux polygon cases.
For the conventional regular polygon example, we can use the polar equation
$$r=\frac{\cos\left(\frac{\pi}{n}\right)}{\cos\left(\left(\left(\theta-\frac{\pi}{n}+\frac{\pi}{2}\right)\bmod \frac{2\pi}{n}\right) -\frac{\pi}{n}\right)}$$
which is a rotated modification of the formula in this Math Stack Exchange answer.
Manipulate[DynamicModule[{road, sol},
sol = NDSolveValue[{\[FormalTheta]'[x] ==
1/ngon[n, \[FormalTheta][x]],
\[FormalTheta][0] == -?/2},
\[FormalTheta], {x, -1, 6}];
road = Plot[-ngon[n, sol[x]], {x, -1, 6}];
Show[road,
Graphics[{{Directive[EdgeForm[GrayLevel[1/4]],
ColorData[97, 3]],
Dynamic[RegularPolygon[{t, 0},
{1, ?/n - ? - sol[t]}, n]]},
{Directive[AbsolutePointSize[6],
ColorData[97, 4]],
Point[Dynamic[{t, 0}]]}}],
AspectRatio -> Automatic, Axes -> None,
GridLines -> {None, {0}},
Method -> {"GridLinesInFront" -> True},
PlotRange -> {All, {-1, 1}}]],
{{n, 4, "sides"}, 3, 12, 1}, {t, 0, 5, Animator},
Initialization :> (ngon[n_Integer, ?_] :=
Cos[?/n] Sec[Mod[? - ?/n + ?/2, 2 ?/n] - ?/n]),
SaveDefinitions -> True, SynchronousUpdating -> False]
Now, let us turn to the Reuleaux polygon case. I (relatively) recently derived a polar equation for the Reuleaux polygons to finally solve a longstanding problem of mine of seeing what the corresponding road for a Reuleaux polygon looks like. The polar equation is understandably a little more elaborate:
$$\small r=\sqrt{1+2\cos\frac{\pi}{n}+\cos^2\left(\left(\left(\theta+\frac{\pi}{2}+\frac{\pi}{n}\right)\bmod{\frac{2\pi}{n}}\right)-\frac{\pi}{n}\right)}-\cos\left(\left(\left(\theta+\frac{\pi}{2}+\frac{\pi}{n}\right)\bmod{\frac{2\pi}{n}}\right)-\frac{\pi}{n}\right)$$
The formula can be compacted a bit in Mathematica by using the three-argument form of Mod[].
Manipulate[DynamicModule[{road, sol, wheel},
sol = NDSolveValue[{\[FormalTheta]'[x] ==
1/reuleaux[n, \[FormalTheta][x]],
\[FormalTheta][0] == -?/2},
\[FormalTheta], {x, -1, 6}];
road = Plot[-reuleaux[n, sol[x]], {x, -1, 6}];
wheel = First[Cases[Normal[PolarPlot[reuleaux[n, ?], {?, 0, 2 ?},
Exclusions -> None]], Line[pts_] :> pts, ?]];
Show[road,
Graphics[{{Directive[EdgeForm[GrayLevel[1/4]], ColorData[97, 3]],
Polygon[Dynamic[
AffineTransform[{RotationMatrix[-?/2 - sol[t]],
{t, 0}}][wheel]]]},
{Directive[AbsolutePointSize[6], ColorData[97, 4]],
Point[Dynamic[{t, 0}]]}}],
AspectRatio -> Automatic, Axes -> None, GridLines -> {None, {0}},
Method -> {"GridLinesInFront" -> True},
PlotRange -> {All, {-1, 1}}]],
{{n, 3, "sides"}, 3, 11, 2}, {t, 0, 5, Animator},
Initialization :> (reuleaux[n_Integer, ?_] :=
Sqrt[1 + 2 Cos[?/n] +
Cos[Mod[? + ?/2, 2 ?/n, -?/n]]^2] -
Cos[Mod[? + ?/2, 2 ?/n, -?/n]]),
SaveDefinitions -> True, SynchronousUpdating -> False]
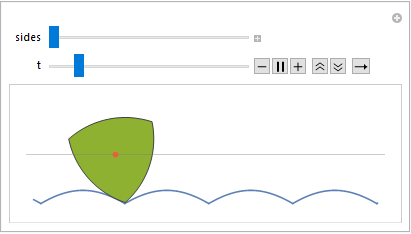
Here is an animation I did much earlier:
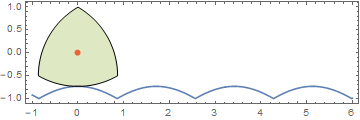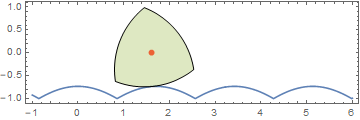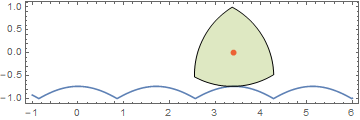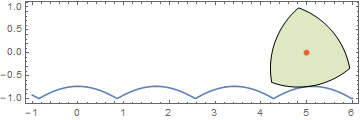
Using the same equation, I tried to derive a closed form for the road, but got stymied when it involved the inversion of the elliptic integral of the second kind, EllipticE[].
 Attachments:
Attachments: