
Catoptric or mirror anamorphoses are deformed images that can only be seen undeformed with the help of a mirror. Here, we experiment with a convex spherical mirror surrounded by a vertical cylindrical surface. We want to compute points of a deformed (anamorphic) image on the cylinder's inner surface such that it is perceived by the viewer as an undeformed image.
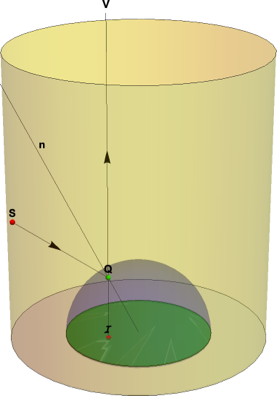
The above drawing shows the anamorphic setup: a spherical mirror (radius r=1), surrounded by a cylindrical surface (radius R>r). The viewpoint V is along the vertical axis of the cylinder (at infinity relative to the size of the sphere). A point S (xa,ya,za) on the cylinder's inner surface is reflected by the mirror at Q to the viewer's eye at V. The viewer perceives the point at I (xi,yi,0). The lines VQ and SQ form equal angles with the normal to the sphere at Q.
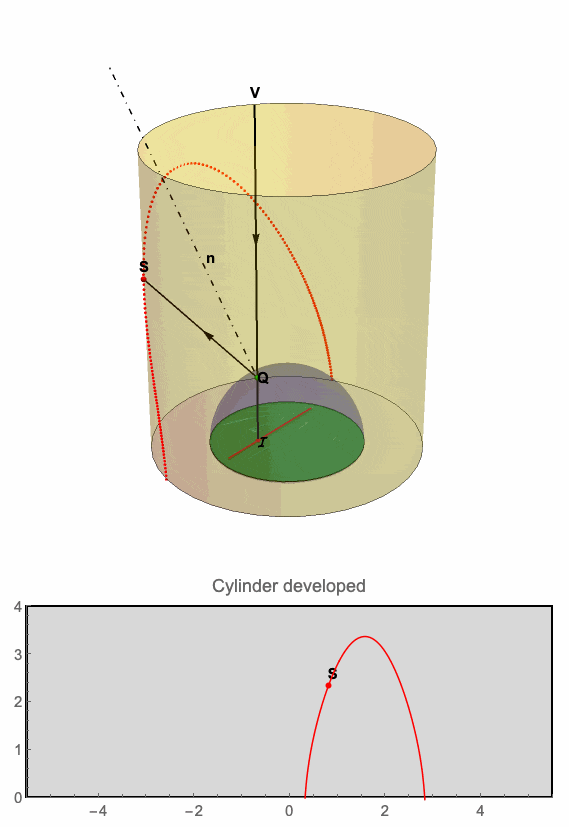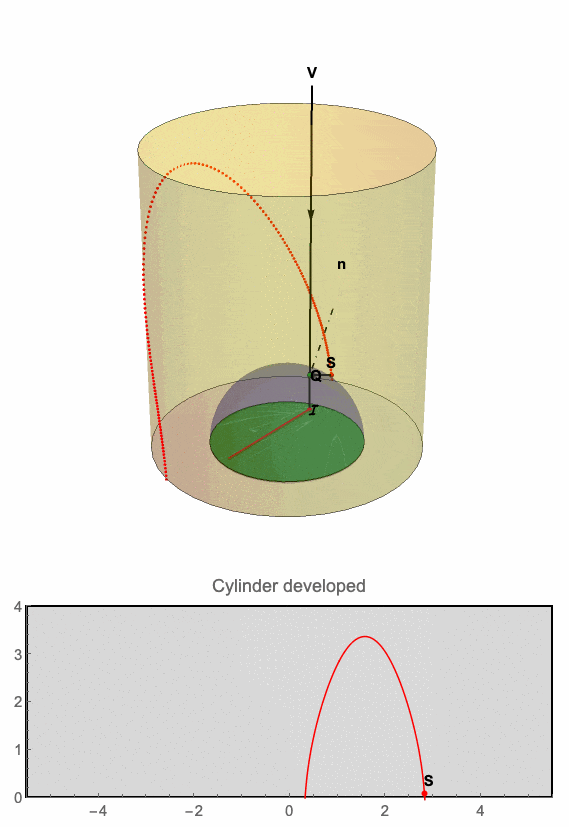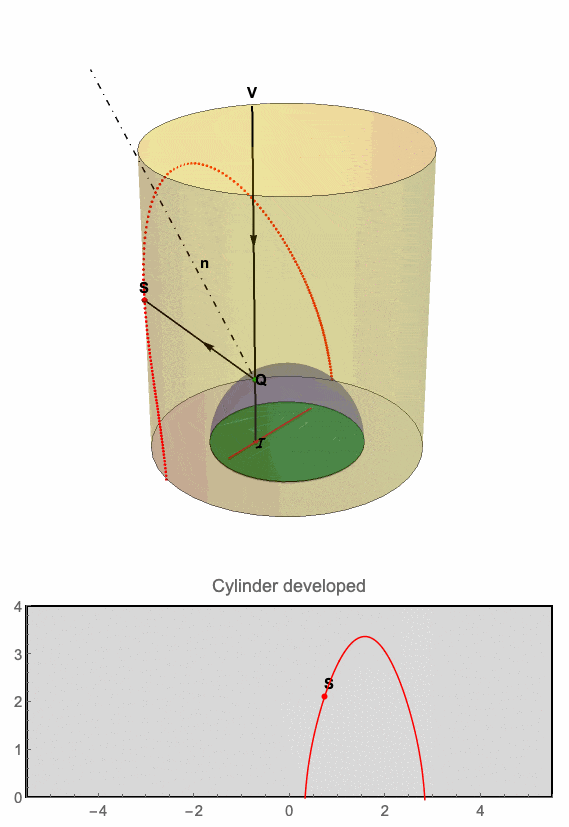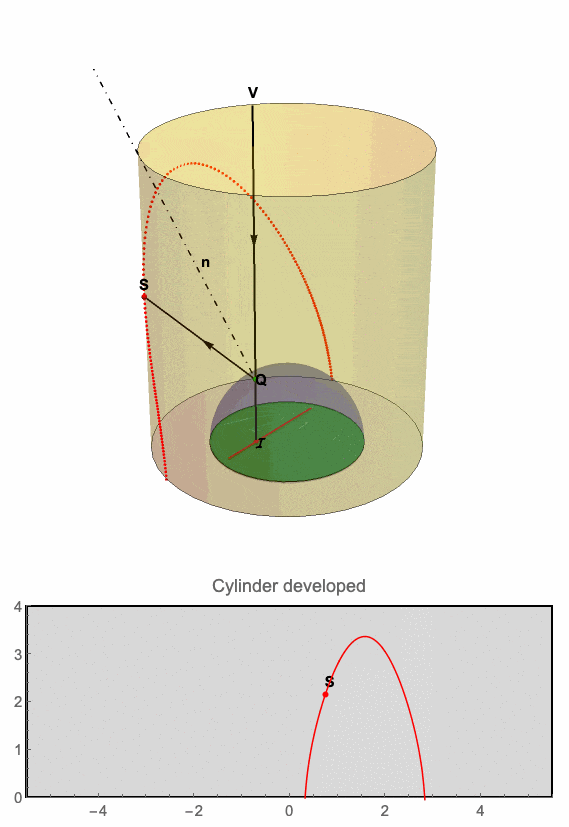
This animation demonstrates the relation between the point I traveling along a straight line while its anamorphic map follows a curve on the inner surface of the cylinder.
We now write a function that expresses this geometric relationship:
sphere2Cylinder[imagePoint : {xi_, yi_}, cylinderRadius : R_] :=
{(R xi)/Sqrt[xi^2 + yi^2], (R yi)/Sqrt[xi^2 + yi^2],
Sqrt[1 - xi^2 -
yi^2] + (R - Sqrt[xi^2 + yi^2]) Cot[2 ArcSin[Sqrt[xi^2 + yi^2]]]}
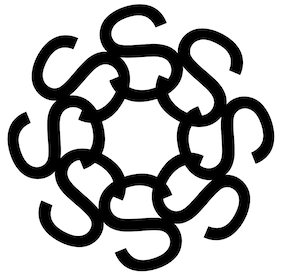
This function maps an image point to an anamorphic point. To test our function, we need a full image as an assembly of many points. We take a circular drawing (logo) to fill the complete bottom of the sphere. Many of these logos can be generated by the Wolfram Demonstration "Character Rotation Patterns" by Chris Carlson.
This is a pasted snapshot from this demonstration's output creating a circular S-logo:
DynamicModule[{letter = 19, offset = 0.53, rotation = 5, n = 8,
upperCase = True},
Graphics[Table[
Rotate[Translate[
Rotate[Text[
Style[FromCharacterCode[If[upperCase, 64, 96] + letter], 300,
FontFamily -> "Arial"], {0, 0}], rotation, {0, 0}], {offset,
0}], r, {0, 0}], {r, 0, 2 \[Pi] - 0.01`, (2 \[Pi])/n}]]];
sun = ImageResize[Binarize@ ImageCrop[%], 950];
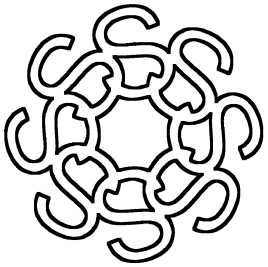
We now convert this image to a GraphicsComplex using ImageGraphics:
ig = ImageGraphics[sun, 2, Method -> "Exact"];
lines = Normal[ig][[1, -1]] /. FilledCurve -> Identity;
scaledLines = Map[#/948 - .5 &, lines, {6}]
Graphics[{Thick, scaledLines}]
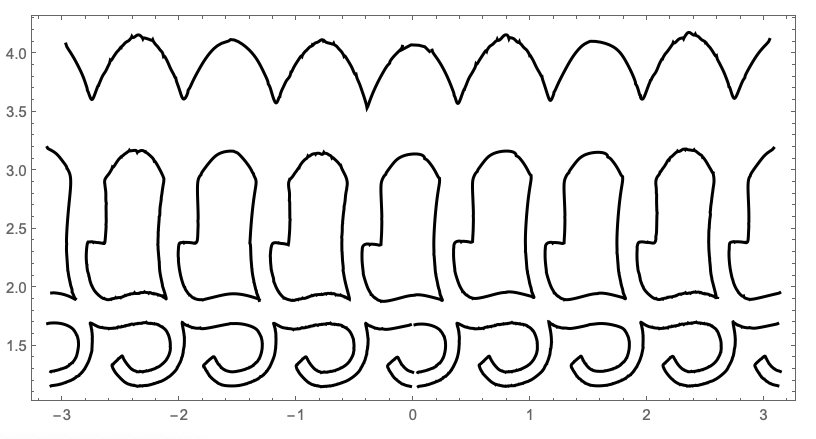
We now convert the point coordinates of the lines in the GraphicsComplex to their anamorphic map {xa,ya,za} using the function sphere2Cylinder. We then convert the anamorphic drawing to the 2 dimensional developed interior face of the cylinder as {ArcTan(xa,ya) , za}.
anaLines = Map[sphere2Cylinder[#, 1.15] &, scaledLines, {5}];
developLineCoordinates =
Flatten[Map[{ArcTan @@ Most[#], Last[#]} &, anaLines, {5}][[-1]],
1][[All, 1]];
Graphics[{AbsoluteThickness[6],
Table[BezierCurve[#, SplineDegree -> 15] & /@
SplitBy[developLineCoordinates[[i]], #[[1]] < 0 &], {i, 1, 10}]},
Frame -> True]
After printing the cylinder development to the right size (50 cm by 20 cm), it is glued around a transparent plastic cylinder (radius 8 cm) and a spherical mirror (a reflecting Christmas ball of radius 7 cm) is put inside at the center. The anamorphic image on the cylinder wall is reflected as the undeformed original by the spherical mirror. Here is the result:
