Please download the attached notebook at the end of the discussion for V12
Dan's blog on automated plane geometry is about a quite fansinating application of new features of V12. This discussion is mainly to show how to make GeometricScene components as building blocks to give you insights to solve challenging geometric problems. Also because the components in this example is quite limited, I hope it serves as beginner case for Wolfram Language users who are interested in applying this feature in teaching and research.
- AOPS Problem: In triangle $ABC$ let point $D$ be on side $BC$. If $AD=7$, $\angle BAD=15$ deg, and $\angle CAD = 30$ deg, compute the minimum possible area of the triangle.
Without further due, lets just start with these very straightforward lines:
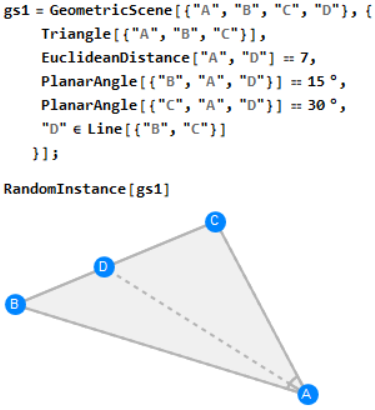
RandomInstance offers a second argument to generate a list of geometric objects that satifies the given concitions
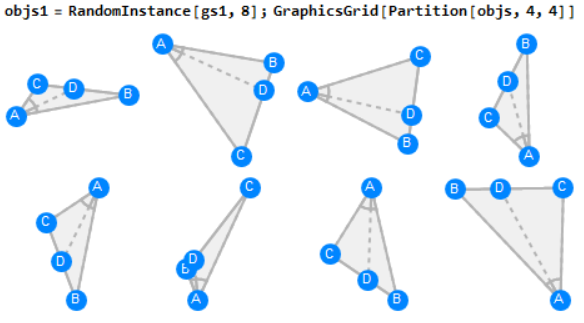
Use the following line to find the area of the triangles above:
In[ ]:= (Area[Triangle[{"A","B","C"}]]/.(#["Points"]))&/@objs1
Out[ ]= {22.0393,21.6971,82.0575,18.1804,90.0952,18.8076,50.7958,25.823}
Lets try more triangles, like 20, and see where is the minimum value even we haven't analyze the problem at all:
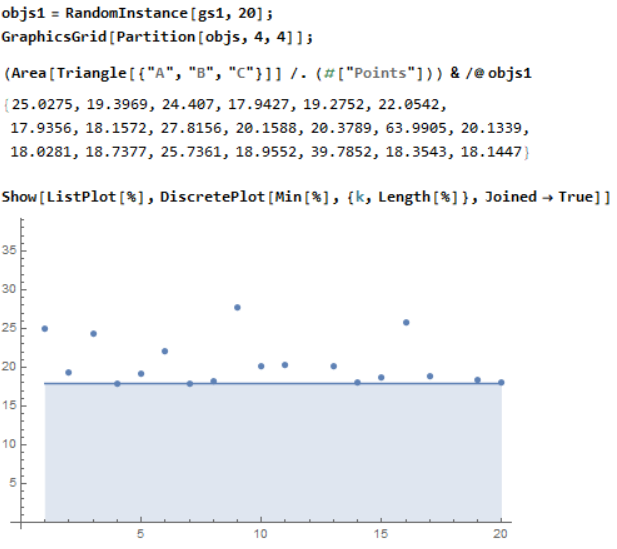
We can graphically conclude that the minimum value is around 17.93. (Pretty good approximation comparing to the true solution later)
Next we consider adding some constraints to the GeometricScences so the illustrations of the valid triangle ABC's are aligned in regularzied manner. Well by the precision of WL and flexibility of MS OneNote, I quitck notice the following works:
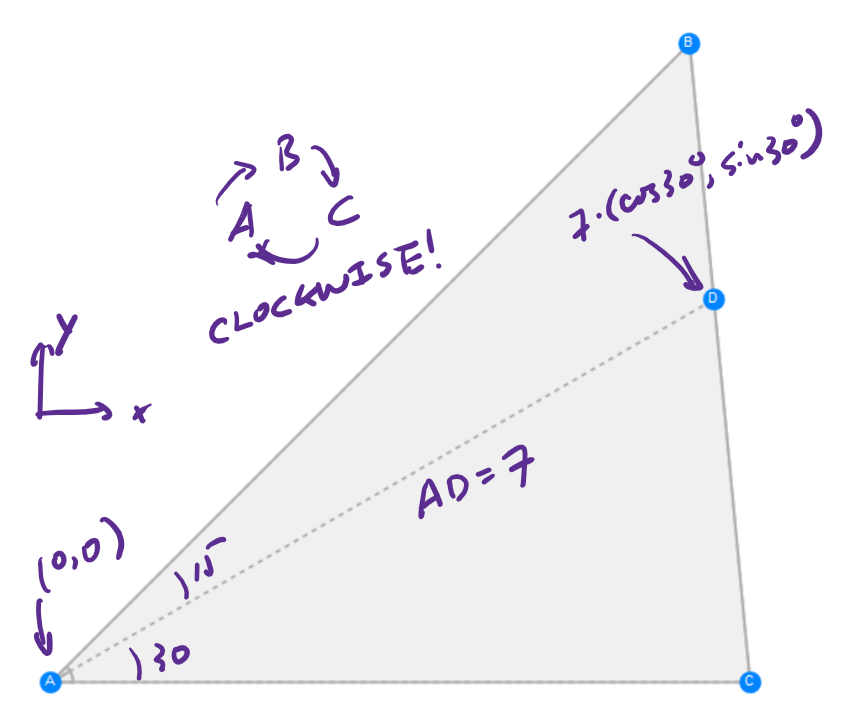
I appriciate that the GeometricScene function gives a mixture of cartesian-coordinate based programming and Geogebra-style freedom. Just modify the first argument in GeometricScene and make 10 instances of valid ABC:
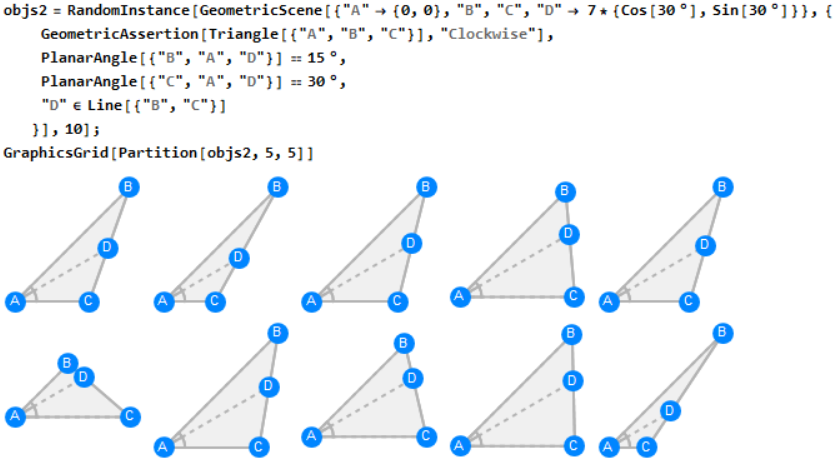
Looking at the the instances, you probably have some insights of the problem. The variation of the area of ABC is by
- fix the angle BAC=45 degree and its two side rays
- rotate a line $l$ that cross point D
$B$, $C$ is then determined by the intersections of rays and $l$. To find how this rotation affects the area, we can parameterize $\angle ABC = \theta$ and the area of ABC. This is valid because $\angle ABD$ is uniquely defined by $\angle ADC$, which can be interpred as a measure of the rotation of $l$.

Comparing to the objs2, we successfully sort the triangles based on the angular size of $\angle ABC$, from 10 degree to 110 degree with increment of 10. Lets plot the area vs $\angle ABC$ on a finer segmentation of angle values:
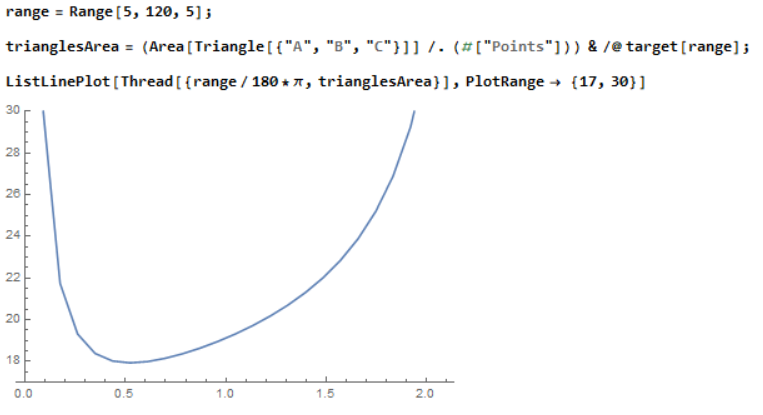
Remember that all codes that you have written is just gs1 plus some plot functions and parameter modification. Almost zero computation but finding the coordinate of $D$. This is way simpler than we used to do with Graphics function.
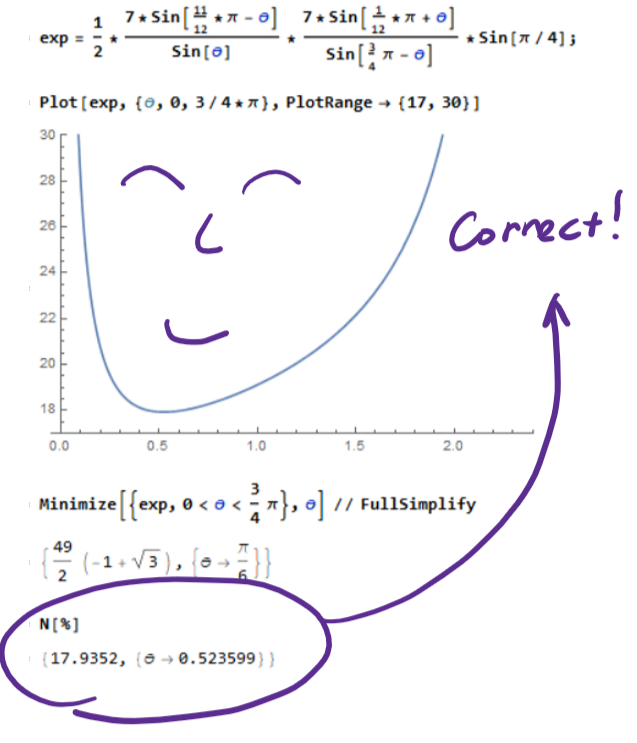
Let's compare our result to the analytic solution:
 Attachments:
Attachments: