GeometricScene and FindGeometricConjectures are two of my favorite new functions in Wolfram Language V12. V12 provides innovative automated capabilities to draw and reason about abstractly described scenes in the plane.
I also remember that I'd proved famous theorems of geometry over many days when I was a junior high school student. I will show nine theorems, including those in the Documentation Center and WOLFRAM blog.
Thaless Theorem
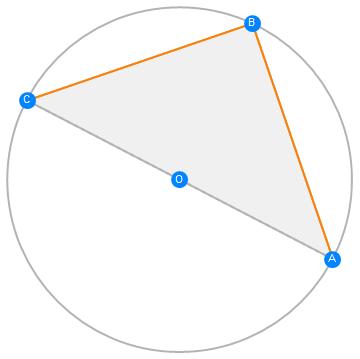
If A, B, and C are distinct points on a circle where the line AC is a diameter, then the angle [Angle]ABC is a right angle.
gs = GeometricScene[{"A", "B", "C", "O"},
{Triangle[{"A", "B", "C"}],
CircleThrough[{"A", "B", "C"}, "O"],
"O" == Midpoint[{"A", "C"}],
Style[Line[{"A", "B"}], Orange],
Style[Line[{"B", "C"}], Orange]
}
];
RandomInstance[gs]
FindGeometricConjectures[gs]["Conclusions"]
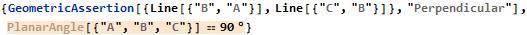
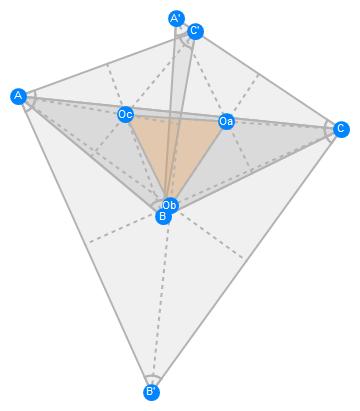
Napoleons Theorem
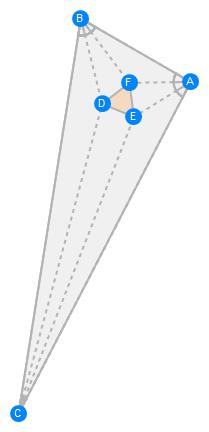
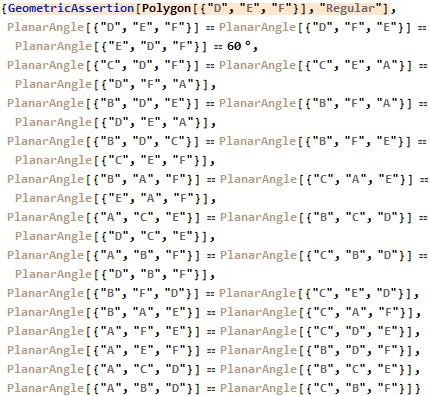
If regular triangles are constructed on the sides of any triangle, either all outward or all inward, the lines connecting the centres of those regular triangles themselves form an regular triangle.
gs = GeometricScene[{"C", "B", "A", "C'", "B'", "A'", "Oc", "Ob",
"Oa"},
{Triangle[{"C", "B", "A"}],
TC == Triangle[{"A", "B", "C'"}],
TB == Triangle[{"C", "A", "B'"}],
TA == Triangle[{"B", "C", "A'"}],
GeometricAssertion[{TC, TB, TA}, "Regular"],
"Oc" == TriangleCenter[TC, "Centroid"],
"Ob" == TriangleCenter[TB, "Centroid"],
"Oa" == TriangleCenter[TA, "Centroid"],
Style[Triangle[{"Oc", "Ob", "Oa"}], Orange]}
];
RandomInstance[gs]
FindGeometricConjectures[gs]["Conclusions"]

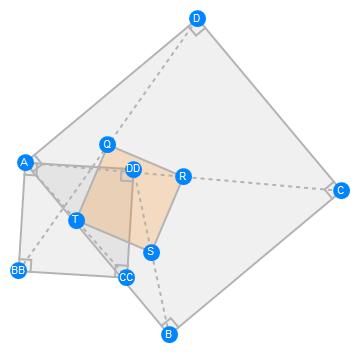
Finsler-Hadwiger Theorem
ABCD and A BB CC DD are two squares with common vertex A. Let Q and S be the midpoints of BB D and DD B respectively, and let R and T be the centers of the two squares. Then the quadrilateral QRST is a square as well.
gs = GeometricScene[{"A", "B", "C", "D", "BB", "CC", "DD", "Q", "R", "S", "T"},
{GeometricAssertion[{Polygon[{"A", "B", "C", "D"}],
Polygon[{"A", "BB", "CC", "DD"}]}, "Regular", "Counterclockwise"],
"Q" == Midpoint[{"BB", "D"}],
"R" == Midpoint[{"A", "C"}],
"S" == Midpoint[{"B", "DD"}],
"T" == Midpoint[{"A", "CC"}],
Style[Polygon[{"Q", "R", "S", "T"}], Orange]}];
RandomInstance[gs]
FindGeometricConjectures[gs]["Conclusions"]

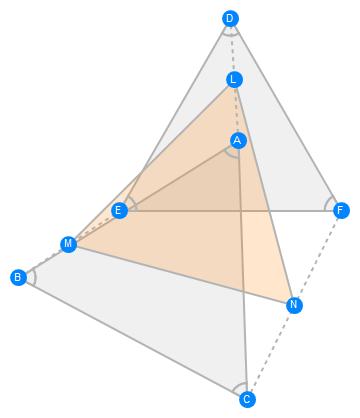
Echols Theorem
The midpoints of AD, BE, and CF in two equilateral triangles ABC and DEF form a regular triangle.
gs = GeometricScene[{"A", "B", "C", "D", "E", "F", "L", "M", "N"},
{T1 == Triangle[{"A", "B", "C"}],
T2 == Triangle[{"D", "E", "F"}],
GeometricAssertion[{T1, T2}, "Regular"],
"L" == Midpoint[{"A", "D"}],
"M" == Midpoint[{"B", "E"}],
"N" == Midpoint[{"C", "F"}],
Style[Triangle[{"L", "M", "N"}], Orange]
}
];
RandomInstance[gs]
FindGeometricConjectures[gs]["Conclusions"]

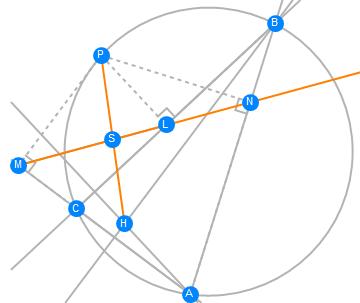
Simson Theorem & Steiner Theorem
Simson's Theorem states that ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. Steiner's Theorem states that if the vertical center of triangle ABC is H, the Simson line passes through the midpoint of PH.
gs = GeometricScene[{"A", "B", "C", "P", "L", "M", "N", "H", "S"},
{CircleThrough[{"P", "A", "B", "C"}],
"L" \[Element] InfiniteLine[{"B", "C"}],
"M" \[Element] InfiniteLine[{"C", "A"}],
"N" \[Element] InfiniteLine[{"A", "B"}],
PlanarAngle[{"P", "L", "B"}] == 90 \[Degree],
PlanarAngle[{"P", "M", "C"}] == 90 \[Degree],
PlanarAngle[{"P", "N", "A"}] == 90 \[Degree],
Style[InfiniteLine[{"L", "M"}], Orange],
GeometricAssertion[{InfiniteLine[{"A", "H"}], Line[{"B", "C"}]},
"Perpendicular"],
GeometricAssertion[{InfiniteLine[{"B", "H"}], Line[{"A", "C"}]},
"Perpendicular"],
Style[Line[{"P", "H"}], Orange],
Line[{"P", "S", "H"}], Line[{"L", "S", "M"}]
}
];
RandomInstance[gs]
FindGeometricConjectures[gs]["Conclusions"]

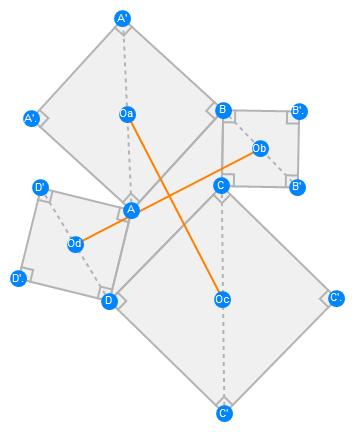
Aubel Theorem
Starting with a given quadrilateral (a polygon having four sides), construct a square on each side.The two line segments between the centers of opposite squares are of equal lengths and are at right angles to one another.
gs = GeometricScene[{"A", "B", "C", "D", "A'", "A''", "B'",
"B''", "C'", "C''", "D'", "D''", "Oa", "Ob", "Oc", "Od"},
{GeometricAssertion[Polygon[{"A", "B", "C", "D"}], "Convex"],
GeometricAssertion[{pa = Polygon[{"A", "B", "A'", "A''"}],
pb = Polygon[{"B", "C", "B'", "B''"}],
pc = Polygon[{"C", "D", "C'", "C''"}],
pd = Polygon[{"D", "A", "D'", "D''"}]}, "Regular",
"Counterclockwise"],
"Oa" == Midpoint[{"A", "A'"}],
"Ob" == Midpoint[{"B", "B'"}],
"Oc" == Midpoint[{"C", "C'"}],
"Od" == Midpoint[{"D", "D'"}],
Style[Line[{"Oa", "Oc"}], Orange],
Style[Line[{"Ob", "Od"}], Orange]}
];
RandomInstance[gs]
FindGeometricConjectures[gs]["Conclusions"]

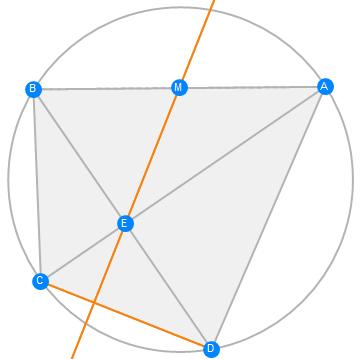
Brahmagupta Theorem
If a cyclic quadrilateral has perpendicular diagonals, then the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side.
gs = GeometricScene[{"A", "B", "C", "D", "E", "M"},
{Polygon[{"A", "B", "C", "D"}],
CircleThrough[{"A", "B", "C", "D"}],
GeometricAssertion[{Line[{"A", "C"}], Line[{"B", "D"}]},
"Perpendicular"],
Line[{"A", "E", "C"}], Line[{"B", "E", "D"}],
"M" == Midpoint[{"A", "B"}],
Style[InfiniteLine[{"M", "E"}], Orange],
Style[Line[{"C", "D"}], Orange]
}
];
RandomInstance[gs]
FindGeometricConjectures[gs]["Conclusions"]

Morley Theorem
In any triangle, the three points of intersection of the adjacent angle trisectors form a regular triangle.
gs = GeometricScene[{"A", "B", "C", "D", "E", "F"},
{Triangle[{"A", "B", "C"}],
PlanarAngle[{"A", "B", "F"}] == PlanarAngle[{"A", "B", "C"}]/3,
PlanarAngle[{"F", "A", "B"}] == PlanarAngle[{"C", "A", "B"}]/3,
PlanarAngle[{"C", "B", "D"}] == PlanarAngle[{"C", "B", "A"}]/3,
PlanarAngle[{"B", "C", "D"}] == PlanarAngle[{"B", "C", "A"}]/3,
PlanarAngle[{"A", "C", "E"}] == PlanarAngle[{"A", "C", "B"}]/3,
PlanarAngle[{"C", "A", "E"}] == PlanarAngle[{"C", "A", "B"}]/3,
"D" \[Element] Triangle[{"A", "B", "C"}],
"E" \[Element] Triangle[{"A", "B", "C"}],
"F" \[Element] Triangle[{"A", "B", "C"}],
Style[Triangle[{"D", "E", "F"}], Orange]
}
];
RandomInstance[gs]
FindGeometricConjectures[gs]["Conclusions"]