Thank you very much. My understanding of probability and statistics is rather rusty. I could really do with a worked example of hypothesis testing for a NonlinearModelFit, to get a feel for what is possible and how it is done.
In my particular case, I have data that I have fitted to a sine curve. The image below, captured from my notebook, shows the data (the dots) with the fitted model (the line). I get an AdjustedRSquared of 0.988181. I would like to know what to make of this.
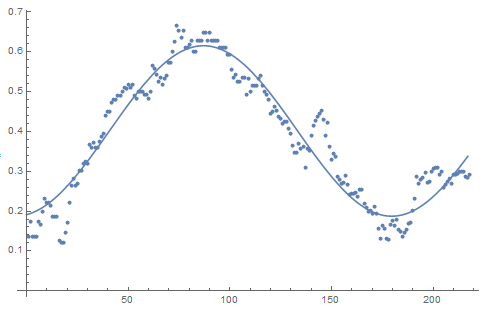
I read that AdjustedRSquared doesn't have the same meaning with a nonlinear as with a linear fit (it's not the percentage of the variation that is explained). Visually, the data seem to fit a sine wave pretty well. But what can I tell people better than just it looks nice? How convinced should we be by this? What basis is there for saying that these data were generated by a sine-like process (plus it looks like some lower amplitude process with irregular oscillations, plus some noise)?
If the null hypothesis were that the data are distributed randomly across the page, I'd imagine that the sine wave comes out as pretty significant. How would I calculate this from NonlinearModelFit's properties? And is that a fair way of doing it? There are 217 data points and 4 parameters (it is fitted to a + b Cos[k x + p]) so lots of degrees of freedom but, on the other hand, it is only just over one cycle of the sine wave. I'd be happy to say that it is a sine wave with a slowly varying period so we don't notice the change over one cycle...