(I have no doubt you read somewhere there there's a difference in meaning in adjusted R2 for linear and nonlinear models. The formula for adjusted R2 only depends on the number of predictor variables. Maybe you're remembering that R2 (adjusted or not) can be more than misleading when the intercept is forced through zero.?)
You don't have to frame everything as a hypothesis test. Getting the standard error of prediction for the mean or of a single new prediction might be a good summary statistic. If the resulting NonlinearModelFit output is stored in nlm. then
nlm["EstimatedVariance"]^0.5
gives you the estimate of the standard error of estimate.
You have to ask yourself (as someone knowing the subject matter) "Is that standard error small enough to satisfy my objectives?" That is a subject matter decision and NOT a statistical decision.
95% Confidence bands for the mean prediction or 95% prediction intervals for an individual prediction are found respectively with
nlm["MeanPredictionBands"]
nlm["SinglePredictionBands"]
You can look at the residuals to check for deviations from the assumptions such as a common variability about the curve and if the pattern of residuals appears to be just a "cloud of points" rather than say the observations in the middle having mostly positive residuals and the extreme lower or upper observations having negative residuals indicating a lack-of-fit.
I've not yet answered your direct question about "testing whether the fit is good". One can perform a test of statistical significance by using the information in the ANOVATable. Again, if the results of NonlinearModelFit are stored in nlm, then
nlm["ANOVATable"]
gets you something like
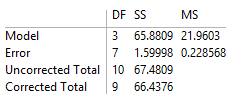
You can grab the information in that table to obtain a P-value for the fit (smaller P-values are associated with better fits than just using the mean of the response variable):
anova = nlm["ANOVATableEntries"]
(* {{3, 65.8809, 21.9603}, {7, 1.59998, 0.228568}, {10, 67.4809}, {9, 66.4376}} *)
fRatio = anova[[1, 3]]/anova[[2, 3]]
(* 96.0777 *)
pValue = 1 - CDF[FRatioDistribution[anova[[1, 1]], anova[[2, 1]]], fRatio]
(* 4.73418*10^-6 *)