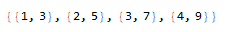Does that help? ... I would do it that way, but I think there must be another way to make it easier...
x = {1, 2, 3, 4};
y = {3, 5, 7, 9};
z = Table[{FromDigits[Take[x, {n}]], FromDigits[Take[y, {n}]]}, {n, 1,
Count[x, _]}]
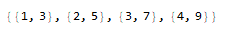
.. or another case..
x2 = {{1, 2}, {2, 4}, {3, 8}, {4, 16}};
y2 = {{3, 6}, {5, 10}, {7, 14}, {9, 18}};
z2 = Table[{FromDigits[Take[FromDigits[Take[x2, {m}]], {1}]],
FromDigits[Take[FromDigits[Take[y2, {m}]], {1}]]}, {m, 1,
Count[x2, _]}]