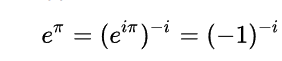One of the most beautiful equations in the whole of mathematics is the identity (and its derivation): 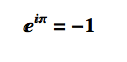
I recently came across another beautiful mathematical concept that likewise relates the two transcendental numbers e and Pi.
We begin by reviewing the concept of a unit sphere, which in 3-dimensional space is the region of points described by the equation: 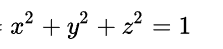
We can some generate random coordinates in Mathematica that satisfy the equation, to produce the expected result: 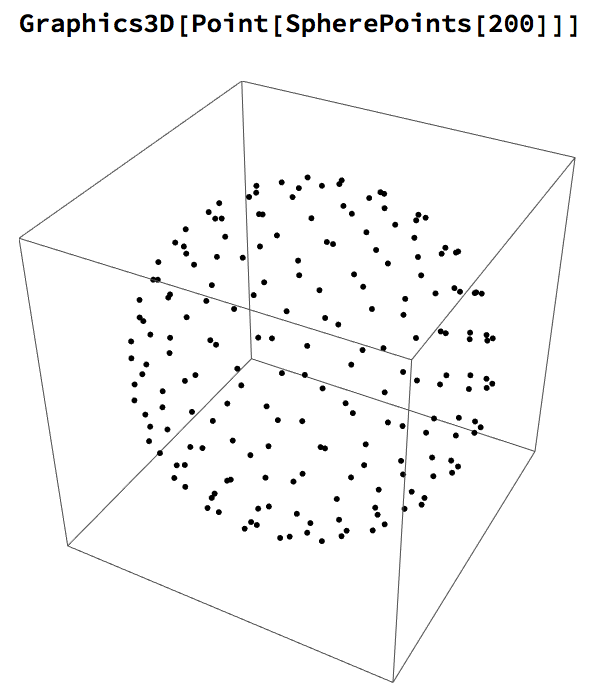
The equation above represents a 3-D unit sphere using the standard Euclidean Norm. It can be generalized to produce a similar formula for an n-dimensional hyper-sphere:
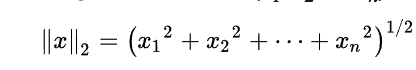
Another way to generalize the concept is by extending the Euclidean distance measure with what are referred to as p-Norms, or L-p spaces:
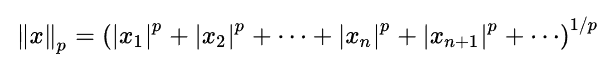
The shape of a unit sphere in L-p space can take many different forms, including some that have corners. Here are some examples of 2-dimensional spheres for values of p varying in the range { 0.25, 4}: 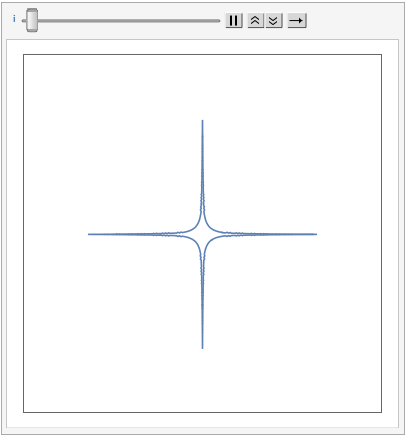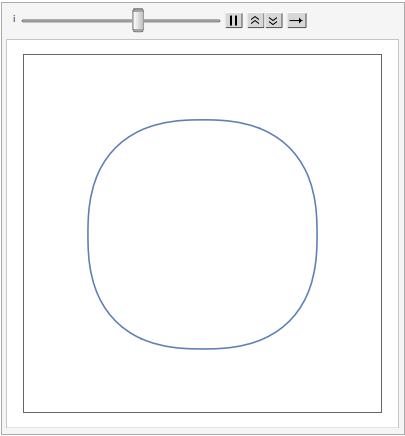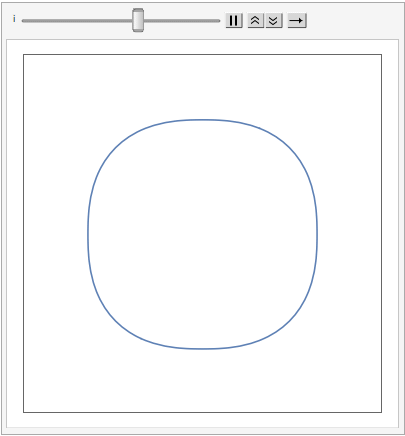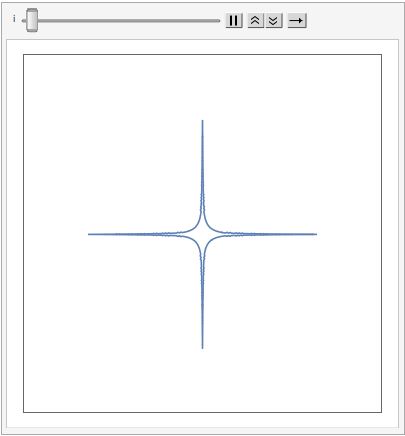
which can also be explored in the complex plane:
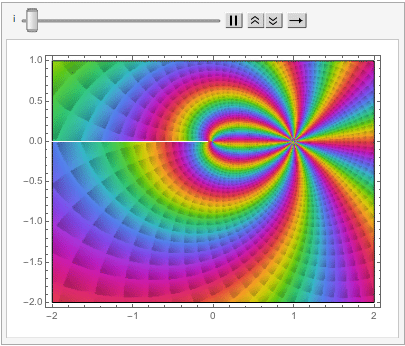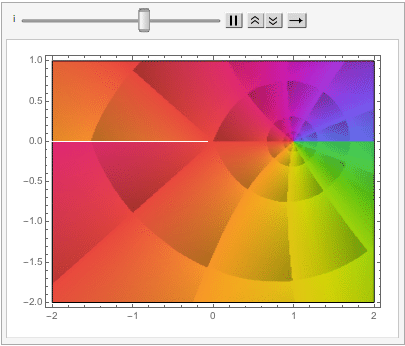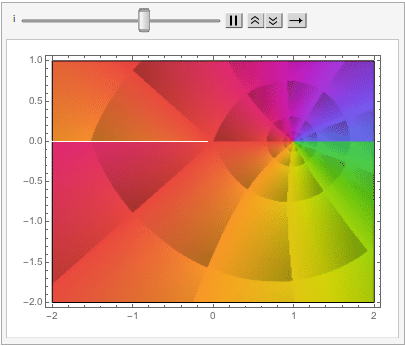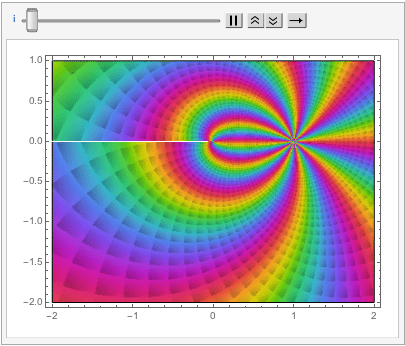
Reverting to the regular Euclidean metric, lets focus on the n-dimensional unit hypersphere, whose volume is given by:
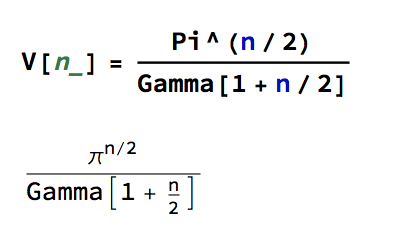
To see this, note that the volume of the unit sphere in 2-D space is just the surface area of a unit circle, which has area V(2) = ?. Furthermore:

This is the equation for the volume of the unit hypersphere in n dimensions. Hence we have the following recurrence relationship: 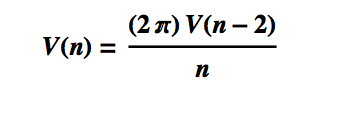
This recursion allows us to prove the equation for the volume of the unit hypersphere, by induction.
The function V(n) take a maximal value of 5.26 for n = 5 dimensions, thereafter declining rapidly towards zero: 
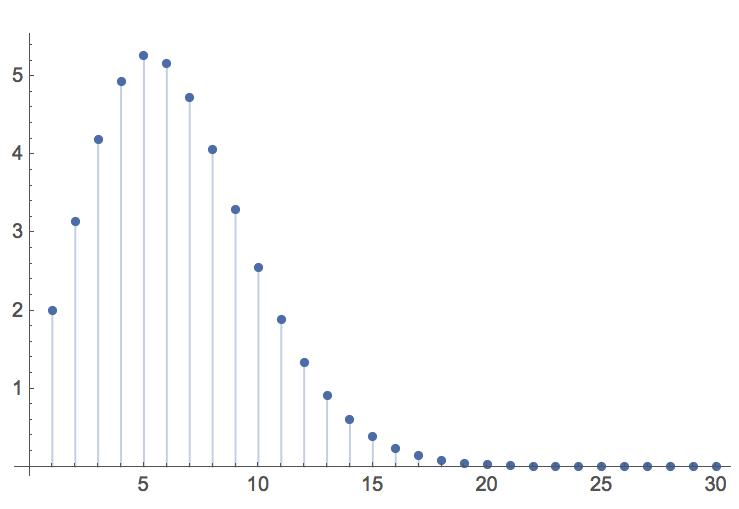
In the limit, the volume of the n-dimensional unit hypersphere tends to zero:

Now, consider the sum of the volumes of unit hypersphere in even dimensions, i.e. for n = 0, 2, 4, 6,
. For example, the first few terms of the sum are:

These are the initial terms of a well-known McClaurin expansion, which in the limit produces the following remarkable result:
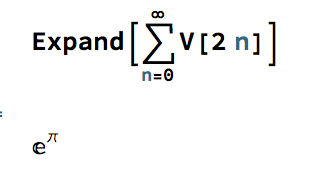
In other words, the infinite sum of the volumes of n-dimensional unit hyperspheres evaluates to a power relationship between the two most famous transcendental numbers. The result, known as Gelfonds constant, is itself a transcendental number: