Missingone square to four, or one equilateral triangle to four.
How about one square to five?
AlgebraicSubstitutionTiling[{1,{{-3,-1},{-3,1},{-1,-3},{-1,-1},{-1,1},{-1,3},{1,-3},{1,-1},{1,1},{1,3},{3,-1},{3,1}}, {{1,6,12,7}-> {{1,2,5,4},{5,6,10,9},{8,9,12,11},{3,4,8,7},{4,5,9,8}}} ,
{{1,1,1,1,1}}},5,{"N", "ImageSize"->{600,Automatic}}]

Here's another one I was just looking at
AlgebraicSubstitutionTiling[{Root[-1-#1^2+#1^3&,1],{{{4,0,0},{0,0,0}},{{8,-4,-1},{0,-8,7}},{{0,0,-4},{0,0,0}},{{0,0,0},{0,0,0}},{{-2,-3,3},{-6,3,1}},{{2,1,-1},{-6,3,1}},{{4,5,-6},{4,1,-2}},{{0,-3,2},{4,1,-2}}}/4, {{1,2,3}-> {{4,7,3},{1,6,4},{6,5,2},{7,8,4},{4,5,6},{2,8,7},{8,5,4},{5,8,2}},
{1,2,3}-> {{1,2,3}},{1,2,3}-> {{1,2,3}},{1,2,3}-> {{1,2,3}},{1,2,3}-> {{1,2,3}},{1,2,3}-> {{1,2,3}},{1,2,3}-> {{1,2,3}}} ,
{{0,2,3,3,4,4,5,5}+1,{1},{2},{3},{4},{5},{6}}},1,{"N", "ImageSize"->{600,Automatic}}]
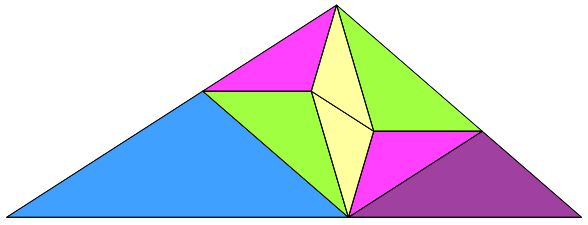
It's in the supergolden ratio, psi. But if you scale the area of the big triangle to the component triangles, you get areas psi^{7.7217, 5, 3, 2, 2, 1, 1, 0, 0} ... the big triangle is out of phase for a smooth substitution tiling system with a fixed number of sizes at each step.