Dear Katherine, I think this is interesting topic. A few thoughts. First let me recommend you a general reading on the subject:
NKS: The Growth of Crystals. Also here is some
WL source code on crystals - some including CA growth. Then if you are interested generally in CAs n non-uniform latices there a few examples at the Demonstration Project:
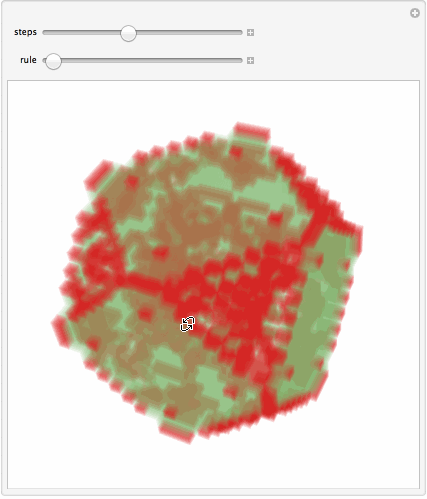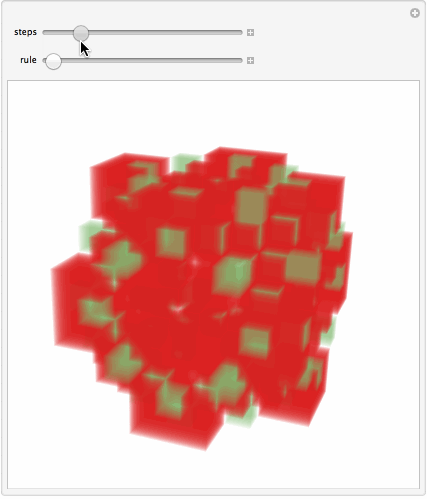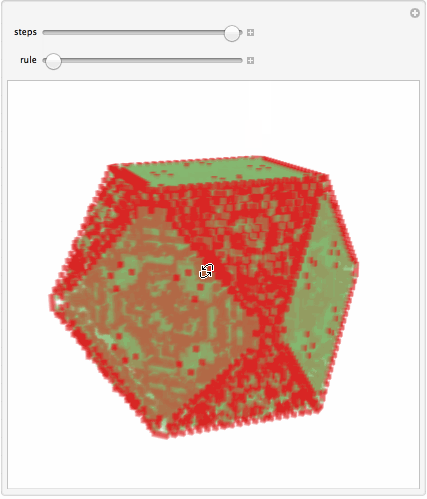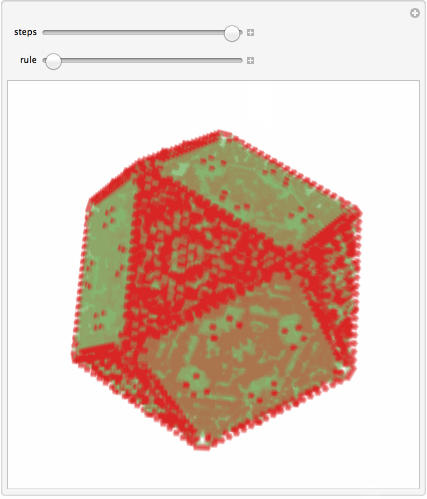
But now sepcifically about binary atom systems, say binary alloys or ionic compounds - say like NaCl. My questions is: are you interested in simulation of such crystal growth in general, or specifically in lattice distortion? Because we can model binary systems not necessarily with differently-sized cells but simply, say, "values" of cells (there could be many other means too). This simple code below is 3-color CA where 2 different types of atoms are represented by red and green. It is not of course a realistic model, just a CA formalism to account for 3 type of things: no atoms, atom type 1, atome type 2.
Manipulate[
Image3D[Last@Rescale[CellularAutomaton[{r, {3, 1}, {1, 1, 1}}, {{{{1}}}, 0}, n]],
ColorFunction -> "RainbowOpacity", ImageSize -> 400, SphericalRegion -> True]
, {{n, 9, "steps"}, 1, 20, 1}
, {{r, 10^8 + 14, "rule"}, 10^8, 10^8 + 10^4, 1}, FrameMargins -> 0]