Abstract

This project is a visualization of Shephard's conjecture, which states that every convex polyhedron admits a self-nonoverlapping unfolding. The conjecture remains unsolved to this day. Currently, there exists unfolding data for several predefined polyhedra in the Wolfram Language, and my goal is to create a function that can do this for any random convex polyhedron. I chose this project because of my love for origami and art, and my interest in 3D visualization.

Generating a Graph for Connectivity Between Faces

The first step was to create a graph that captures the relationship between faces of the polyhedron so that it could be used later to generate the net. The built-in function DualPolyhedron converts the polyhedron to one where each vertex corresponds to a face on the original. I then extracted the vertices of the dual polyhedron and partitioned and sorted them, allowing me to create a graph using those vertices.

polyhedronfacegraph[polyhedron_]:= 

    Block[{dualpolyhedron, vertexlist, vertexpairings, sortedvertices},

    dualpolyhedron = DualPolyhedron[polyhedron];  
    vertexlist = dualpolyhedron[[2]];   

    vertexpairings = Flatten[Table[Append[

       Partition[vertexlist[[n]], 2, 1], 
       {Last[vertexlist[[n]]], First[vertexlist[[n]]]}],  
       {n, 1, Length[vertexlist]}], 1];

    sortedvertices = Sort /@ vertexpairings // DeleteDuplicates; 

        Graph[UndirectedEdge@@@sortedvertices,VertexLabels -> "Name"] 
]

A random polyhedron and the graph of its dual:

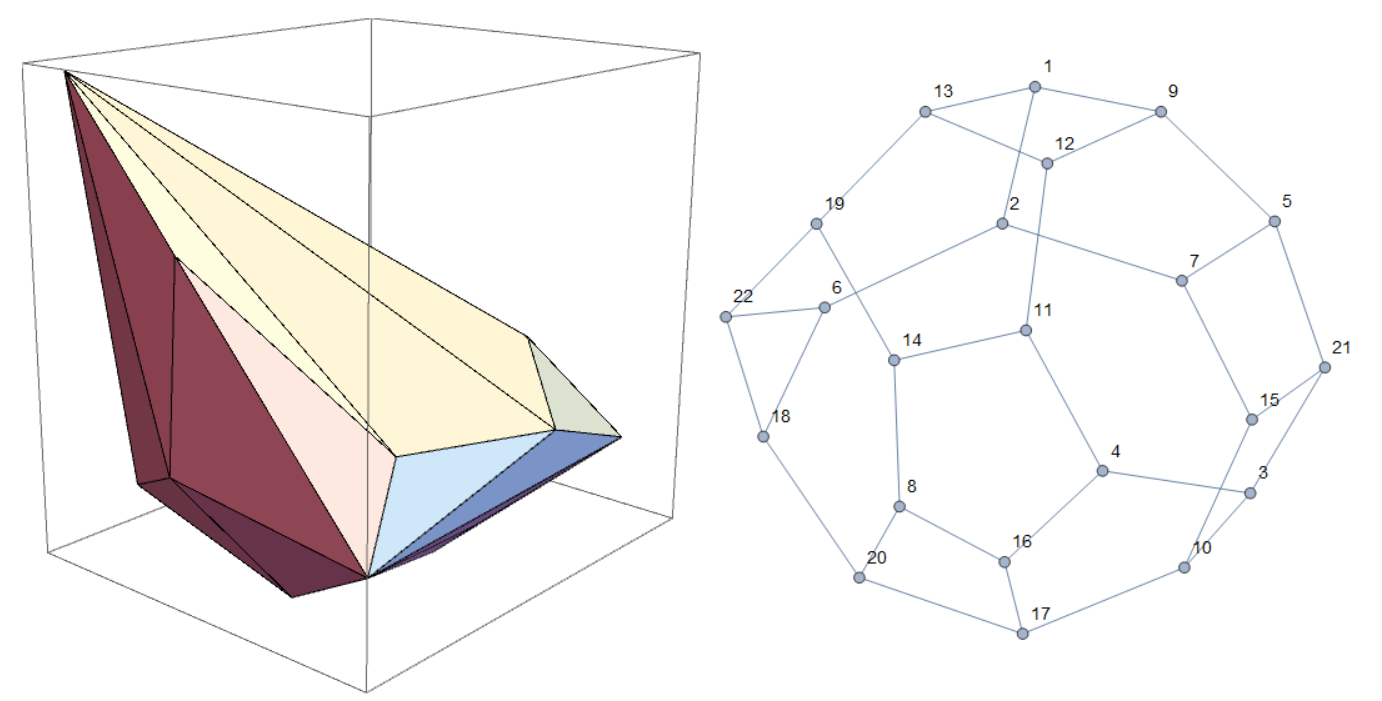
Generating Spanning Trees

I then used the graph to generate different paths in which a polyhedron could unfold. One way to do this is by using a spanning tree, a tree generated from a graph that retains the same amount of vertices while having the minimum amount of edges. This essentially creates a simple version of what the final net should look like. Each vertex represents a face, and connections between them signify that they are adjacent. It is important to note that not every spanning tree will correspond to a non-overlapping net, which is why I generate a spanning tree from every possible vertex.

generatetrees[graph_] := Table[FindSpanningTree[{graph, n}], {n, 1, VertexCount[graph]}]

Five of the spanning trees of the previous polyhedron:

Generating Net Coordinates

To create the net of the polyhedron, I had to implement an unfolding algorithm. My first approach was to extract each face individually, but that ended up complicating the transformations. My final algorithm consisted of applying one transformation to move one face to the xy plane, then unfolding using connections between vertices from the spanning tree.

I first created a function to find the normal vector to a plane using the cross product.

normvector[coords_] := Cross[coords[[2]] - coords[[1]], coords[[3]] - coords[[1]]];  

I then use transformation matrices so that one face is lying on the xy plane, and convert the new mesh into a list of its primitives. The next step is to begin unfolding the polyhedron from its bottom face using the list of spanning trees. To perform an algorithm on each step of the unfolding process, I use the function BreadthFirstScan, which can call the unfold function (discussed next) whenever a new vertex is reached. Finally, the function returns a list of coordinates of the completed net.

generatenetcoords[mesh_, tree_]:=

    Block[{transformations, transformedmesh, meshlist, transformedmeshlist, normals, polygonfaces, transformedrotation},

       polygonfaces = Reap[

         meshlist = MeshPrimitives[mesh, 2][[All, 1]];

         transformations =      
         RotationTransform[{normvector[meshlist[[1]]], {0, 0, -1}}] @*   
         TranslationTransform[-PropertyValue[{mesh, {2, 1}}, MeshCellCentroid]];  

         transformedmesh = TransformedRegion[mesh, transformations];      
         transformedmeshlist = MeshPrimitives[transformedmesh, 2][[All, 1]];     

         normals = normvector[#] &/@ transformedmeshlist;    

         Sow[transformedmeshlist[[1]], "flat"];

         transformedrotation[1] = TransformationFunction[IdentityMatrix[4]];

         BreadthFirstScan[tree, 1, "DiscoverVertex" -> unfold[transformedmeshlist, normals, transformedrotation]];,  
         {"flat"}][[-1, All, 1]];
       Chop[polygonfaces]
]

The unfold function operates by finding the intersection of two polygons, calculating the angle between them, and applying transformations using normal vectors to unfold the face. The function returns coordinates of the transformed polygons.

unfold[meshlist_, normals_, transformedrotation_][u_, v_, _] /; (u =!= v) :=

    Block[{edgecoord1, edgecoord2, angle, rotation},

    {edgecoord1, edgecoord2} = Intersection @@ meshlist[[{u, v}]]; 
    angle = DihedralAngle[{edgecoord1, edgecoord2}, normals[[{u, v}]]];
    rotation = RotationTransform[angle, edgecoord2 - edgecoord1, Mean[{edgecoord1, edgecoord2}]];

    transformedrotation[u] = transformedrotation[v] @* rotation;
    Sow[transformedrotation[u] @ meshlist[[u]], "flat"];
]

Generating Possible Nets

Finally, we put all the functions together. The program iterates through every spanning tree to produce nets using netcoordinates. The third element of each coordinate is deleted to convert the net to 2D. Each net is then tested for overlap by calculating the surface area of the original polyhedron and comparing it to the surface area of the net. Only nets where the two surface areas are equal are appended to the list that is returned.

generateallnets[polyhedron_] := 

    Block[{netcoords, trees, graph, mesh, surfacearea, netsurfacearea, goodnets},

    mesh = BoundaryDiscretizeGraphics[polyhedron];   
    graph = polyhedronfacegraph[polyhedron];
    trees = generatetrees[graph];

    goodnets = {};   

    Table[     
        netcoords = First@generatenetcoords[mesh, trees[[treeposition]]];    
        netcoords = Table[Delete[netcoords[[n, m]], {3}], {n, 1, Length[netcoords]}, {m, 1, 3}];        

        surfacearea = SurfaceArea[polyhedron];
        netsurfacearea = RegionMeasure[RegionUnion[Polygon /@ netcoords]];

        If[surfacearea == netsurfacearea,             
           AppendTo[goodnets, Graphics[{Hue[0.94, 0.22, 1.], EdgeForm[{Thin, Pink}], Polygon /@ netcoords}]]        
        ];,  

        {treeposition, 1, Length[trees]} 
    ];    

    Row[{Graphics3D[polyhedron], goodnets}]
]

Outputs

Upon taking a polyhedron object in as its argument, the final output of the function is a 3D graphic of the original polyhedron and a list of all possible nets.

An output of a random polyhedron:

Summary

With the help of my mentor, I was able to create a program that creates non-overlapping nets for random polyhedra. The process consisted of extracting graphs, creating spanning trees, generating nets, and checking for overlap. The function returns several successful results for every random polyhedron that I tested, although the program does run quite slowly for polyhedra with high numbers of faces, as the complexity of the graph and number of spanning trees increase drastically as the number of faces increase. From this project, I acquired knowledge of many aspects of three-dimensional modeling and geometric transformations, and I hope to work on extensions of this project in the future.

Future Work

A possible extension would be applying a similar algorithm to non-convex polyhedra and showing that it is impossible to generate a non-overlapping net in some cases. Additionally, optimization algorithms could also be implemented to speed up the unfolding process. For example, another function could also be created to generate the first net that is valid, which would greatly increase speed if only one net is desired.

Acknowledgements

I would like to sincerely thank my mentor, Jeremy Stratton-Smith, for providing invaluable advice and help throughout the entire project process. I would also like to thank Chip Hurst for his unfolding algorithm and tips for 3D transformations. Lastly, I would like to thank the Wolfram Summer Camp team for providing me with this opportunity to pursue a project of my choice.