Introduction

I've been studying Latin since eighth grade (I'm currently going into twelfth), and every year I fall more in love with the language. Last school year, I took AP Latin and was immediately drawn to the complex world of Latin poetry. At the same time, I entered an Artificial Intelligence class and continued to develop a passion for computer science. The idea of coding something to do with Latin (especially with poetry) has been simmering in my mind for a while, and I finally came up with and created this project over the past two weeks at camp.

Many significant works of Latin poetry follow the format of dactylic hexameter, meaning that every line is composed of some combination of six metrical feet, each of which is either a spondee (two long syllables) or a dactyl (one long syllable followed by two short syllables). The determination of the length of each syllable is based on the word itself, its position in the line, and the surrounding words and metrical feet. Scansion is the process of identifying the pattern of metrical feet in a line of Latin poetry. Having a quick way to scan lines makes reciting Roman poetry aloud easier, allowing an audience beyond just "Latin people" to appreciate the beauty of Latin rhythmical patterns, as well as the beauty of the language itself. In this project, I used machine learning to scan lines of Latin poetry in dactylic hexameter.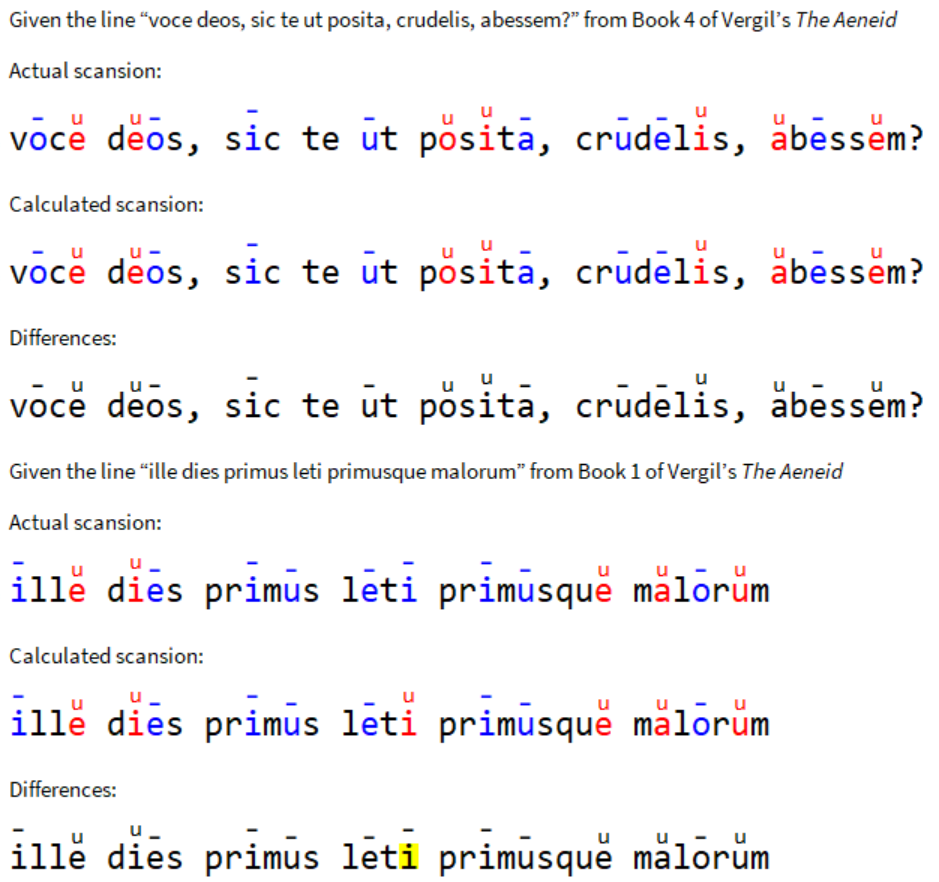

Scansion

Latin poetry primarily uses two types of metrical feet: spondees, or two long syllables, and dactyls, or one long syllable followed by two short syllables. Different meters mandate varying quantities of total feet or of specific types of feet. In dactylic hexameter, the last two of the six total feet are almost always a dactyl and a spondee, and the first four can be either dactyls or spondees. The rest of the feet are determined using a series of rules and eventually process of elimination. Because the syllable lengths and endings of each word change based on its function in a sentence, scansion becomes complicated to automate by simply using a Latin dictionary.

A few basic rules for understanding the result of the project: - Some vowels are designated long or short by nature of the word itself - Diphthongs are always long - Vowels followed by two consonants are usually long - When a word ending with a vowel (or a vowel and the letter "m") is followed by a word starting with a vowel (or the letter "h" and a vowel), the last syllable of the first word "disappears" in what's called an elision

Method

I originally planned to implement automatic scansion using the rules I'd learned in Latin class. However, I already knew how I could accomplish that, and, ultimately, I came to camp to learn and to explore coding in the Wolfram Language, not to do something I could have done at home. Hence, I embarked on an exciting (and probably less successful objectively) journey through neural networks in the Wolfram Language.

After finding and parsing data, I experimented with four different input/output combinations when developing my neural network and fiddled around with the numbers and layers for each. I ended up using a sequence-to-sequence network with an input of a line of text and an output of a list of probabilities that each character will be a long vowel; short vowel; or consonant, punctuation mark, or ignored vowel. From there, I converted the neural network output into a color-coded line with metrical markings.

Data

I got training data from AP Latin resources on scanning Vergil's The Aeneid on www.hands-up-education.org. The lines included syllabic length and metrical foot breaks and were formatted as such: "?rm? v?r|?mqu? c?n|?, || Tr?|ia? qu?| pr?m?s ?b| ?r?s."

After removing markings for metrical feet, I converted the line and its markings into a list of integers (one for each character) in which 1 indicated a long vowel; 2 a short vowel; and 3 a consonant, punctuation mark, or ignored vowel. I then converted the file into a list of rules with the plain line leading to its associated list of character "lengths."

formatData[lines_]:=Table[plainLine[x] -> allCharLengths[removeFootMarks[x]],{x, lines}]

Here is an example of a data point I used:

"Hinc via Tartarei quae fert Acherontis ad undas"-> {3,1,3,3,3,3,2,2,3,3,1,3,3,2,3,2,1,3,3,3,3,1,3,3,1,3,3,3,2,3,3,2,3,1,3,3,2,3,3,2,3,3,1,3,3,1,3}

Neural Network

I used 824 lines as my training data and 20 lines as my testing data. I trained a sequence-to-sequence neural network. I varied the EmbeddingLayer argument and the MaxTrainingRounds in order to find the best combination. I ended up using on 12 and 100.

net=NetChain[{EmbeddingLayer[12], NetBidirectionalOperator[LongShortTermMemoryLayer[32]], NetMapOperator[LinearLayer[3]],SoftmaxLayer[]}, "Input"-> NetEncoder[{"Characters",{{"!","(",")",".",",",";","?",":",""",""", "-"}->1," ",CharacterRange["a","z"], _}, "IgnoreCase"-> True}]]
result = NetTrain[net, trainingData, All, LossFunction->CrossEntropyLossLayer["Index"], ValidationSet->testData, MaxTrainingRounds->1000]

The neural network I obtained had a error of 2.9% on the validation data, so an incorrectly classified character appears every few lines.

Formatting the Neural Network Output

The neural network outputs a list of probabilities of 1, 2, and 3 for each character like this:

{{0.233388, 0.747286, 0.0193251}, {0.0237603, 0.102153, 
  0.874087}, {0.000247855, 0.00735917, 0.992393}, {0.0196234, 
  0.932275, 0.0481015}, {0.000736693, 0.0109938, 
  0.98827}, {0.000217165, 0.00133861, 0.998444}, {0.912511, 0.0845969,
   0.00289202}, {0.00648514, 0.0000726016, 0.993442}, {0.941853, 
  0.00259834, 0.0555489}, {0.000389534, 0.0000140205, 
  0.999596}, {0.000185425, 0.000205691, 0.999609}, {0.00244669, 
  0.0108199, 0.986733}, {0.165211, 0.616111, 0.218678}, {0.000199178, 
  0.0000279639, 0.999773}, {0.0000528181, 3.42483*10^-6, 
  0.999944}, {0.920206, 0.000883119, 0.0789105}, {0.00396218, 
  8.48394*10^-7, 0.996037}, {0.992206, 0.0000137013, 
  0.00778067}, {0.00125184, 5.09544*10^-7, 0.998748}, {0.000426706, 
  1.91505*10^-6, 0.999571}, {0.000130377, 4.82552*10^-6, 
  0.999865}, {0.0000298044, 9.46518*10^-6, 0.999961}, {0.172772, 
  0.0202387, 0.80699}, {0.942826, 0.0060539, 0.05112}, {0.30773, 
  0.0000756251, 0.692195}, {0.850813, 0.000620744, 
  0.148566}, {0.000179449, 3.39269*10^-6, 0.999817}, {0.0000538242, 
  0.00011357, 0.999833}, {0.000553092, 0.0406213, 
  0.958826}, {0.00931922, 0.985319, 0.00536204}, {0.0000223564, 
  0.000134355, 0.999843}, {0.00933962, 0.0149729, 
  0.975688}, {0.000112443, 0.000270864, 0.999617}, {0.470264, 
  0.527769, 0.00196643}, {0.000150167, 0.0000335595, 
  0.999816}, {0.239256, 0.209718, 0.551026}, {0.0000601962, 
  0.000211833, 0.999728}, {0.0000575157, 0.00195887, 
  0.997984}, {0.0931677, 0.556272, 0.35056}, {0.00254616, 0.00115129, 
  0.996302}, {0.0340716, 0.00185011, 0.964078}, {0.987841, 0.00371802,
   0.00844058}, {0.0313373, 0.000806895, 0.967856}, {0.752181, 
  0.226585, 0.021234}, {0.00223789, 0.00123329, 0.996529}}

I formatted the probabilities into a list of the most probable integers for each character.

calcOutput[probs_]:= Table[If[Max[x] == x[[1]], 1, If[Max[x] == x[[2]], 2, 3]], {x, probs}]

From the list of integers, I formatted and color-coded the newly scanned line.

markings = {Style["-", Bold], Style["u", Smaller]}
overscripts[line_, lengths_] := 
 scannedLine = 
  Table[If[lengths[[x]] == 3, StringPart[line, x], 
    Overscript[StringPart[line, x], markings[[lengths[[x]]]]]], {x, 
    Range[Length[lengths]]}]
colors[line_, lengths_] := ( 
  newLine = 
   Table[If [lengths[[x]] == 3, line[[x]], 
     Style[line[[x]], If[lengths[[x]] == 1, Blue, Red]]], {x, 
     Range[Length[lengths]]}];
  Style[Row[newLine], Large]
  )

Final Product

Given a line, the program guesses the syllabic pattern and outputs the color-coded line with markings.

scan[line_]:=(
out = calcOutput[trainedNet[line]];
colors[overscripts[line, out], out]
)

Conclusions and Future Extensions

Through this project, I was able to create a neural network that successfully determines and formats the metrical pattern of lines of Latin poetry in dactylic hexameter (2.9% error). The program takes a plain line of poetry and outputs the resulting color-coded line with metrical markings.

In the future, markings between metrical feet could be added to the displayed lines. The program could also be extended to other types of meter or to poetry in other languages.

Acknowledgements

I would like to thank my wonderful mentor, Christian Pasquel, for his endless support throughout the process. I would also like to thank the other Wolfram Summer Camp mentors and the Wolfram Summer School mentors and students.