Introduction
I first became interested in cellular automata when I learned about Conway's Game of Life, and I was interested in the Wolfram Language's machine learning and graphics, so I was very excited for this project! The 3D Cellular Automata project uses machine learning to classify the general shape of 3D models generated by cellular automata and specifically looks for rules that generate irregular shapes. In order to achieve my goals, I trained a function to recognize familiar shapes like spheres and cubes from 3D models that have the general shape of the 3D figures. Additionally, I generated both a training and testing set of cellular automata models to run through the machine learning. Also, a function that uses the rules of specific cellular automata has been constructed to generate the locations of each cell.

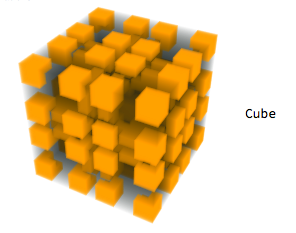
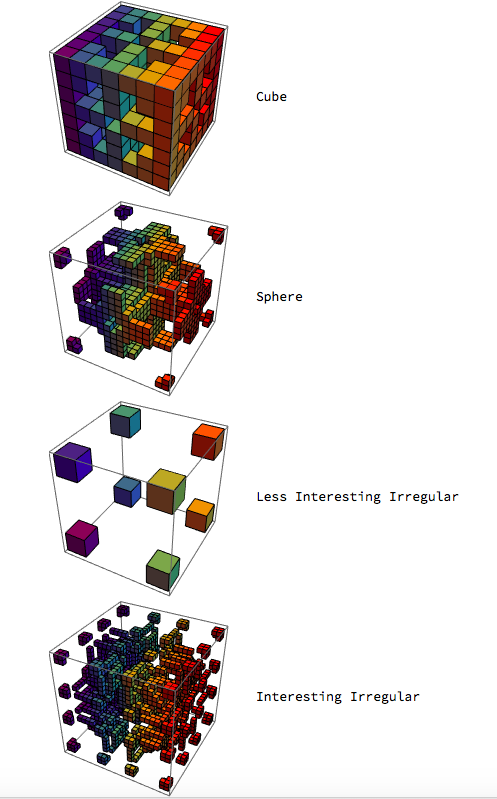
The end result of my code is a classification of cellular automata with the possible classifications of Cube, Sphere, Interesting Irregular, and Less Interesting Irregular.
What are Cellular Automata?
A cellular automaton is a set of rules iteratively applied to a configuration of cells. This means that the automaton changes during each iteration as the states of the cells change based on the rules. For example, if one cell is alive at the beginning and the rule is to change a cell to become alive if its neighboring cells are alive, then in the next iteration the four cells next to the first cell will be alive.

Rules 0-255 are a set of deterministic rules for cellular automata. In my project, I only study rules 2-254 going up by 4 since these rules operate on the idea that each cell has two possible states.
3D Cellular Automata
To generate the figures made by cellular automata, I used the CellularAutomaton function in the Wolfram Language. This function returns a list of lists with numbers, so the Image3D function is used to make the output into an image. Therefore, I made the following function to generate the 3D models of cellular automata, and I used it to make both the test and training set.
caVal[{n_, k_, t_}] :=
Image3D[#, ImageSize -> 100] & /@
CellularAutomaton[{n, {k, 1}, {1, 1, 1}}, {{{{1}}}, 0}, {{t}}]

I also used code from "A New Kind of Science" and Wolfram Documentation to generate other 3D cellular automata.

Machine Learning
To make the training set, I used a Manipulate to generate figures using cellular automata. Then, I classified the figures based on their shape. At first, I had Cube, Sphere, and Irregular as the classes. However, after meeting with Stephen Wolfram, we decided to divide the Irregular class into Less Interesting Irregular and Interesting Irregular. The purpose of this was to filter out models that were not intriguing to examine (they were just not a cube or a sphere). Thus, the possible classes are Cube, Sphere, and Interesting Irregular, and Less Interesting Irregular.
Manipulate[
Image3D[#, ImageSize -> 250] & /@
CellularAutomaton[{x, {2, 1}, {1, 1, 1}}, {{{{1}}}, 0}, {{t}}], {x,
k2rules[[Key[2]]]}, {t, 2, 35, 1}]
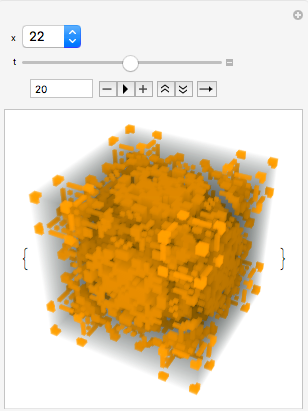
To make the training data, I stored each figure and its classification in an association.
tST = Join[
Thread[sT -> Table["Sphere", Length[sT]]],
Thread[cT -> Table["Cube", Length[cT]] ],
Thread[IIT -> Table["Interesting Irregular", Length[IIT]]] ,
Thread[IBT -> Table["Less Interesting Irregular", Length[IBT]]]
]
Association values for interesting irregular class. 
Next, I put the training set into the Classify function with the PerformanceGoal of Quality to make the machine learning function.
totalisticClassifier = Classify[tST, PerformanceGoal -> "Quality"]
After testing the function and looking at information on it, I found that it classified figures constructed according to cellular automata rules with 87% accuracy.


Also, I wrote functions to return only the cellular automata models of a particular classification.
interesting[n_] := Cases[n, {_, "Interesting Irregular"}] // TableForm
lessInteresting[n_] :=
Cases[n, {_, "Less Interesting Irregular"}] // TableForm
cube[n_] := Cases[n, {_, "Cube"}] // TableForm
sphere[n_] := Cases[n, {_,"Sphere"}] // TableForm
 (with // Row instead of // TableForm)
(with // Row instead of // TableForm)
Extensions
I created functions that make it easier for a user to classify figures generated by cellular automata rules.
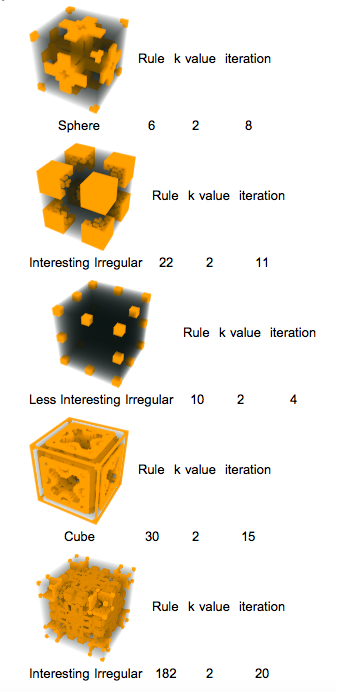
I made a function that returns the classification of the 3D representation of the cellular automata rule in a specific iteration when given a list with the rule number, k value, and desired iteration.
classifyRI[{r_, k_, i_}] := {Image3D[#, ImageSize -> 200] & /@
CellularAutomaton[{r, {k, 1}, {1, 1, 1}}, {{{{1}}}, 0}, {{i}}]} //
totalC
Furthermore, I made a function that returns a figure generated by cellular automata with its classification, rule number, k value, and iteration!
dataDisplay[{n_, k_, t_}] := {Text[
Grid[{{caVal[{n, k, t}] // TableForm, "Rule", "k value",
"iteration"}, {caVal[{n, k, t}] // totalisticClassifier, n, k,
t}}]]} // TableForm
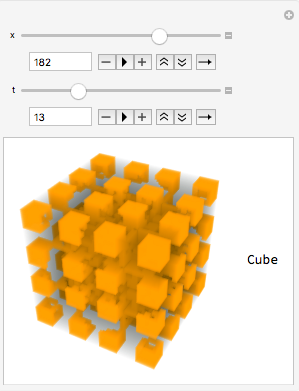
Additionally, I made a Manipulate so that the 3D cellular automata shapes can be classified in a user friendly way.
Manipulate[classifyRI[{x, 2, t}], {x, 2, 254, 4}, {t, 0, 50, 1}]
Rainbow
My mentor, Sylvia Haas, helped me make a Manipulate to display 3D cellular automata in rainbow colors!
Manipulate[
Graphics3D[
Riffle[Table[
ColorData["Rainbow", c], {c, 0, 1, 1/Length[#]}], #] & [
Cuboid /@ Position[#, 1]] & /@
CellularAutomaton[{x, {2, 1}, {1, 1, 1}}, {{{{1}}},
0}, {{t}}]], {x, k2rules[[Key[2]]]}, {t, 2, 35, 1}]
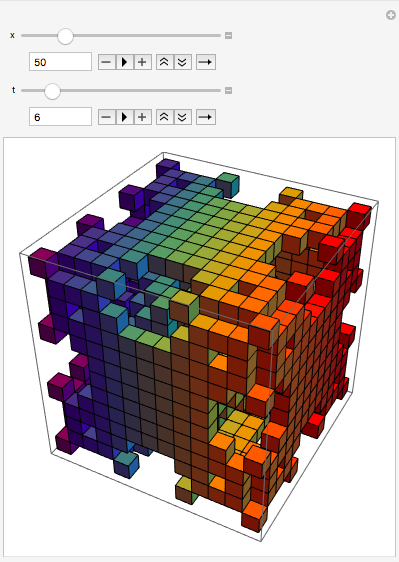
I then made a function that returns classified models in rainbow colors! First, I made a function that returned figured generated by cellular automata in rainbow colors.
rainbow[n_, k_, t_] :=
Graphics3D[
Riffle[Table[
ColorData["Rainbow", c], {c, 0, 1, 1/Length[#]}], #] & [
Cuboid /@ Position[#, 1]] & /@
CellularAutomaton[{n, {2, 1}, {1, 1, 1}}, {{{{1}}}, 0}, {{t}}]]
I used this function and the classifying function to return an output with rainbow cellular automata and a classification!
rainRI[{n_, k_, t_}] := Grid[{{rainbow[n, k, t], totalisticClassifier[caVal[{n, k, t}]]}}]
Summary
The 3D Cellular Automata project has a machine learning function that can classify 3D cellular automata iterations as cubes, spheres, less interesting irregulars, and interesting irregulars with 87% accuracy. The classification is specifically for iterations of rules 2 - 254 going up in steps of 4 with the k value being 2, meaning that each cell can be in two different states. The classifier was tested with 20 iterations of all the cellular automata rules that have k values of 2. Using this function, classifications for different iterations of cellular automata with the same rule can be compared to find patterns in the evolving shape. I also wrote a function that displays only the cellular automata with a particular classification. For example, one could see only the cubes in a set. To make classifying cellular automata easier for the user, the program has many different functions that can be used to classify rules. There is a function that classifies figures for a specific rule number and iteration, or for a rule number and a range of iterations. In addition, a function generating animations for the evolution of each cellular automata rule and a Manipulate displaying the cellular automata figure in rainbow colors have been created. The project's classification found that the rules 22 and 182 have a high amount of interesting irregular figures!
Future Work
In the future, I would like to classify figures for states other than 2. This would mean that k could equal 3, 4, or any other number. Furthermore, the current model classifies based on shapes created when one cell is alive in the beginning and the rest are null. In the future, the classification would include figures created with more than one live cell at the start so that cellular automata figures from different starting configurations of the same rule can be compared. Additionally, the current model includes only four different classes: cube, sphere, less interesting irregular, and interesting irregular. With the future development of the project, there would be more classes like rectangular prisms, which would be added with the varying starting configurations. Furthermore, I would like to develop a function to classify the cellular automata by the patterns of their iterations. For example, if over time a pattern repeats, it would be a repetitive rule.

Acknowledgements
Thank you to my amazing mentor, Sylvia Haas, for providing me with support during the entire process! Also, thank you to all of the mentors at Wolfram Summer Camp for helping me!
Github link: https://github.com/adriennewlai21/WSS-Template