Here is a way that allows you to parametrized the family in terms of one of the standard bases for the space of polynomials. Let the basis be called
B. The basis
B may be specified by one of the built-in functions, such as
HermiteH,
Laguerre, etc., or by a user-defined function. An augmented matrix for the linear equations defined a polynomial passing through given points is contructed in terms of coordinates with respect to the basis
B.
The linear system is solved via
RowReduce and
NullSpace is used to find a basis for the null space. The basis for the null space, whose vectors are
B-coordinate vectors, is multiplied by parameters, a table of
Slot, which are used to construct a function that takes parameters as its input and returns the corresponding polynomial function.
Examples
In:
interpolatingFamily[{{-1, 4}, {0, 2}, {1, 6}}, 4, "basis" -> HermiteH]
Out:
Function[{x}, 2 + x (1 - 8 #1 + x (3 - 16 #2 + x (8 #1 + 16 x #2)))] &
In:
interpolatingFamily[{{-1, 4}, {0, 2}, {1, 6}}, 4, "basis" -> HermiteH][1, 2]
Out:
Function[{x}, 2 + x (1 - 8 1 + x (3 - 16 2 + x (8 1 + 16 x 2)))]
In:
interpolatingFamily[{{-1, 4}, {0, 2}, {1, 6}}, 4, "basis" -> HermiteH][1, 2][x]
Out:
2 + x (-7 + x (-29 + x (8 + 32 x)))
In:
interpolatingFamily[{{-1, 4}, {0, 2}, {1, 6}}, 4, "basis" -> HermiteH][a, b][x] // Collect[#, x] &
Out
2 + (1 - 8 a) x + (3 - 16 b) x^2 + 8 a x^3 + 16 b x^4
Code:
ClearAll[basis, interpolatingFamily];
Options[basis] = {"reverseDegree" -> False};
basis::usage =
"basis[deg,var,basisFunction,opts] returns a basis up to degree deg in the variable var";
basis[deg_Integer, var_, "powers", opts : OptionsPattern[]] :=
basis[deg, var, Power[#2, #1] &, opts];
(* for HermiteH, LaguerreL, etc. *)
basis[deg_Integer, var_,
fn : Except[_Rule | RuleDelayed] : (Power[#2, #1] &),
opts : OptionsPattern[]] :=
fn[#, var] & /@
If[TrueQ@ OptionValue["reverseDegree"], Range[deg, 0, -1], Range[0, deg]];
interpolatingFamily::usage =
"interpolatingFamily[pts, deg, opts] returns a polynomial function \
iFam[a, b, ...][x] with parameters a, b, ... that interpolates pts";
Options[interpolatingFamily] = {"basis" -> "powers", "reverseDegree" -> False};
interpolatingFamily[pts_?MatrixQ, deg_Integer, opts : OptionsPattern[]] /; deg + 1 >= Length@pts :=
Module[{mat, y0, aug, solCoords, b},
Block[{x},
b = basis[deg, x, OptionValue["basis"], FilterRules[{opts}, Options[basis]]];
mat = (b /. x -> First[#]) & /@ pts;
y0 = Last /@ pts;
aug = Transpose[Transpose[mat] ~Append~ y0];
solCoords = Last /@ RowReduce@aug;
Evaluate[
Function @@ {
{x},
HornerForm[
solCoords.Take[b, Length@ pts] +
If[deg < Length@ pts,
0,
Table[Slot[i], {i, deg + 1 - Length@pts}] . Reverse@ NullSpace[mat].b],
x]}
] &
]]
A
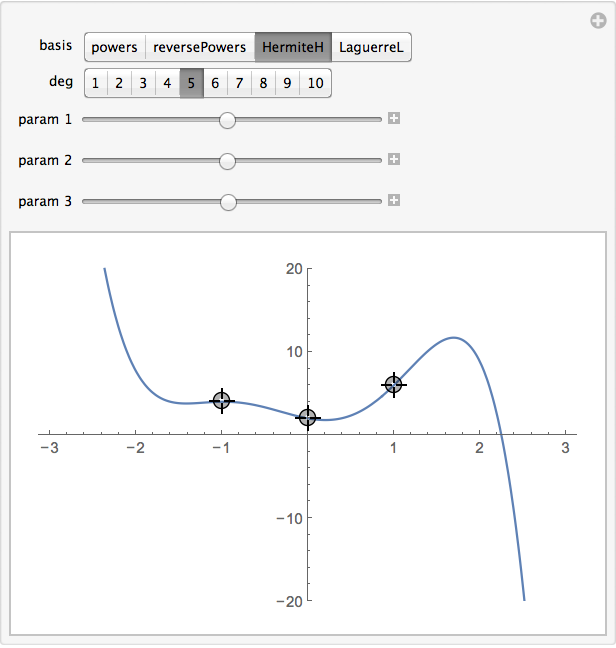
Manipulate toy:
Manipulate[
deg = Clip[deg, {Length@pts - 1, Length@pts + 2}];
Plot[
Evaluate@
interpolatingFamily[pts, deg, "basis" -> basis][p1, p2, p3][x],
{x, -3, 3},
PlotRange -> 20],
{{pts, {{-1, 4}, {0, 2}, {1, 6}}}, Locator, LocatorAutoCreate -> True},
{{basis, HermiteH}, {"powers", "reversePowers", HermiteH, LaguerreL}},
{{deg, 4}, Range[1, 10], SetterBar},
{{p1, 0, "param 1"}, -1, 1}, {{p2, 0, "param 2"}, -1, 1}, {{p3, 0, "param 3"}, -1, 1}
]