A few years ago, I introduced Object-Oriented-Programming environment for Wolfram language with no packages. Today, I would like to introduce a new type of Wolfram OOP. Previous one is the type of Method-preceded style, and new one is Instance-preceded style.
Key function of Method-preceded style is UpSetDelayed function that combines method to instance, and for the Instance-preceded style is SetDelayed function. There is a small deference between Method-preceded and Instance-preceded, but more easy style may be Instance-preceded one.
I already shown a fundamental class definition of Method-preceded style as,
class[nam_]:= Module[{local},
localValueGetMethod[nam]^:= local;
localValueSetMethod[nam[x_]]^:= local= x;
]
A new fundamental class definition of Instance-preceded style is as follows.
class[nam_]:= Module[{local},
nam[localValueGetMethod]:= local;
nam[localValueSetMethod[x_]]:= local= x;
]
From the class, we can make a instance as,
class[instance]
Then we can set a value to the inner-variables as,
instance[localValueSetMethod[10]]
We get a result "10". Also, we can call the inner-variables as,
instance[localValueGetMethod]
We can get the value "10". The construction of instance is equal to evaluate a class function with the name of instance, we can use Map to produce multiple instances as,
objectList = {instance1, instance2};
Map[class, objectList];
Each style is being applicable the Association function for the Construction and message handling for multiple objects as previously shown in my articles.
Next sample is to animate 3-dimensional objects movement using Instance-preceded OOP for Wolfram language.
DynamicModule[{
n = 10,
speed = 0.01,
speedRange = {1., 5.},
bg = ParametricPlot3D[{(2 + Cos[8 u]) Cos[u], (2 + Cos[8 u]) Sin[u], Sin[8 u]}, {u, 0, 2 Pi},
PlotRangePadding -> 0.3, PlotStyle -> {Thickness[0.005]}, Axes -> None],
objectList},
CLASS DEFINITION;
new[nam_] := Module[{u = 0, v = 1},
nam[setv[x_]] := v = x;
nam[step]:= (u++; s = u*v; {Specularity[White, 20],
Sphere[{(2 + Cos[8 s]) Cos[s], (2 + Cos[8 s]) Sin[s], Sin[8 s]}, .25]})
];
CREATE INSTANCES;
objectList = Table[Unique[], {n}];
Map[new[#]&, objectList];
Map[#[setv[speed*RandomReal[speedRange]]] &, objectList];
SHOW GRAPHICS;
movingPoints3D := Graphics3D[{Map[#[step] &, objectList]}];
Animate[t;
Show[{bg, movingPoints3D}], {t, 0, 100, 1}, AnimationRunning -> False]
]
We can see the animation of 3D spheres as following image.
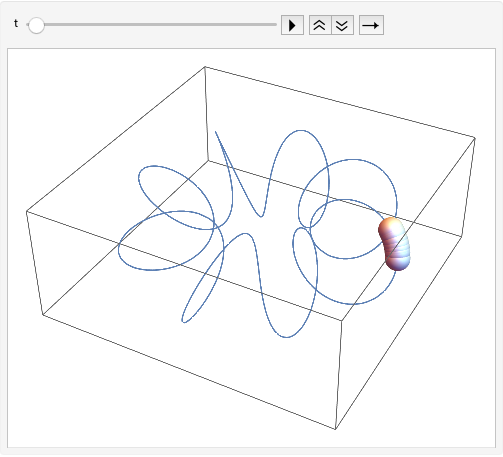
Enjoy, Wolfram Object Oriented Programming!