A few years ago, I introduced Object-Oriented-Programming environment for Wolfram language with no packages. Today, I would like to introduce a new type of Wolfram OOP. Previous one is the type of Method-preceded style, and new one is Instance-preceded style.

Key function of Method-preceded style is UpSetDelayed function that combines method to instance, and for the Instance-preceded style is SetDelayed function. There is a small deference between Method-preceded and Instance-preceded, but more easy style may be Instance-preceded one.

I already shown a fundamental class definition of Method-preceded style as,

class[nam_]:= Module[{local},
    localValueGetMethod[nam]^:= local;
    localValueSetMethod[nam[x_]]^:= local= x;
    ]

A new fundamental class definition of Instance-preceded style is as follows.

class[nam_]:= Module[{local},
   nam[localValueGetMethod]:= local;
    nam[localValueSetMethod[x_]]:= local= x;
    ]

From the class, we can make a instance as,

class[instance]

Then we can set a value to the inner-variables as,

instance[localValueSetMethod[10]]

We get a result "10". Also, we can call the inner-variables as,

instance[localValueGetMethod]

We can get the value "10". The construction of instance is equal to evaluate a class function with the name of instance, we can use Map to produce multiple instances as,

objectList = {instance1, instance2};
Map[class, objectList];

Each style is being applicable the Association function for the Construction and message handling for multiple objects as previously shown in my articles.

Next sample is to animate 3-dimensional objects movement using Instance-preceded OOP for Wolfram language.

DynamicModule[{
  n = 10,
  speed = 0.01,
  speedRange = {1., 5.},
  bg = ParametricPlot3D[{(2 + Cos[8 u]) Cos[u], (2 + Cos[8 u]) Sin[u], Sin[8 u]}, {u, 0, 2 Pi},
   PlotRangePadding -> 0.3, PlotStyle -> {Thickness[0.005]}, Axes -> None],
  objectList},

 CLASS DEFINITION;
 new[nam_] := Module[{u = 0, v = 1},
   nam[setv[x_]] := v = x;
   nam[step]:= (u++; s = u*v; {Specularity[White, 20],
    Sphere[{(2 + Cos[8 s]) Cos[s], (2 + Cos[8 s]) Sin[s], Sin[8 s]}, .25]})
   ];

 CREATE INSTANCES;
 objectList = Table[Unique[], {n}];
 Map[new[#]&, objectList];
 Map[#[setv[speed*RandomReal[speedRange]]] &, objectList];

 SHOW GRAPHICS;
 movingPoints3D := Graphics3D[{Map[#[step] &, objectList]}];
 Animate[t;
  Show[{bg, movingPoints3D}], {t, 0, 100, 1}, AnimationRunning -> False]
 ]

We can see the animation of 3D spheres as following image.

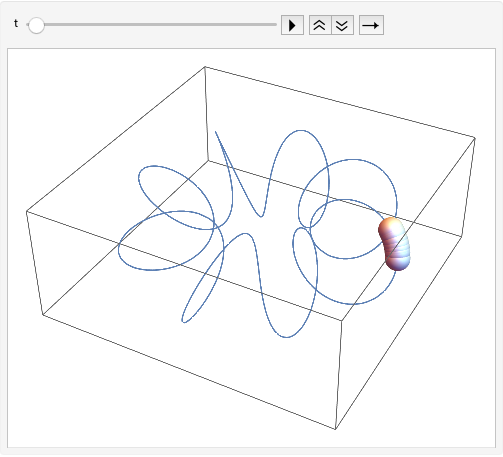
Enjoy, Wolfram Object Oriented Programming!