Hello community.
I am studying different ways to find the diagonal of a matrix without using the Diagonal command, just for an operations study, of course I can use Diagonal[], but I wonder if there is a way to simulate this command using other commands, just so that I can learn more about the WL language.
For example the matrix a (10000 x 10000) defined by:
SeedRandom[1234]
n = 10000;
a = Table[RandomInteger[9, n], n];
To have a basis of comparison for the study, I get the performance of the Diagonal command:
Diagonal[a]; // AbsoluteTiming
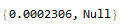
Some attempts (all were slower than Diagonal[]):
Map[a[[#, #]] &, Range@n]; // AbsoluteTiming

Table[a[[i, i]], {i, Length@a}]; // AbsoluteTiming
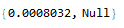
I think I've found a better way than the ones I've tried so far:
Extract[Table[{i, i}, {i, Length@a}]][a]; // AbsoluteTiming

But it still takes about more than twice the time of Diagonal[].
What other ways to find the diagonal of a matrix that are faster than these attempts above without using the Diagonal command? I would love to learn other ways, I could only think of those two ways. Could it also be that, even using Part, there is a faster and simpler way that I haven't thought of? Can anyone teach me others ways (even if they are slower than Diagonal[])? I will be very grateful if anyone can help! Thanks.