There is no simple rule between the prime number $p_n$ and the next prime number $p_{n+1}$ that cannot be predicted. Similarly, the interval between the twin prime number $Tp_n$ and the next twin prime number $Tp_{n+1}$ cannot be predicted. Considering two twin primes as a set of four primes $\{p_{m1},p_{p1},p_{m2},p_{p2}\}$, it can be described as $Tp_1=\{p_{m1},p_{p1}\}$ and $Tp_2=\{p_{m2},p_{p2}\}$.

Here, it is assumed that there are no other twin prime numbers between $Tp_1$ and $Tp_2$. The difference between $p_{m2}$ and $p_{p1}$ is defined as$"{\rm interval}"$. When the first prime number $p_{m1}$ is specified, the other three prime numbers are defined by equation $(1)$.

$$Tp_1= \{p_{m1},p_{p1}\}?{\rm interval}?Tp_2=\{p_{m2},p_{p2}\}$$

$$\begin{eqnarray} {\rm interval}&=&p_{m2}-p_{p1}\\ p_{p1}&=&p_{m1}+2\\ p_{m2}&=&p_{p1}+{\rm interval}\tag{1}\\ p_{p2}&=&p_{m2}+2\\ \end{eqnarray}$$

Look at the following graph.

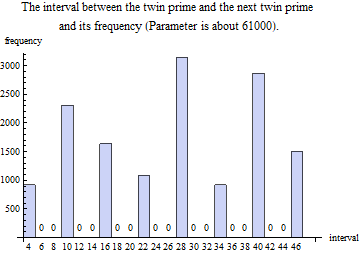
The horizontal axis of this graph is the "${\rm interval} $" (=$p{m2}-p{p1} $) of the twin prime $Tp_1$ and the next twin prime $Tp_2$. The vertical axis is the frequency of occurrence, and the parameter is approximately 61000. What you can see in the graph is the fact that there is a solution only if the "${\rm interval} $" is $4,10,16,22,?$. In the case of $6,8,12,14,?$ there is no solution. I will omit the explanation, but this is because one or both of $Tp_2$ is not a prime number depending on the condition of equation ( $1$). (the sum of odd and odd numbers is even, multiples of 3 are involved)

Here we introduce a variable $r$ representing "${\rm interval} $". In equation ($2$), $r$ takes an integer value only when "${\rm interval} $" is $4,10,16,22, ?$.

$$\begin{eqnarray} r=\frac{1}{6}\times{\rm interval}+\frac{1}{3}\tag{2} \end{eqnarray}$$

$$\begin{equation}r=1,2,3\cdots\end{equation}$$

The purpose of this report is to give $r$ an "${\rm interval}$" and search for a set of twin primes that satisfy that condition. Twin prime numbers can be determined by the following four equations.

$$\begin{eqnarray} n&=&6 s_1^2+(6 s_1-1)(m_1-1)\tag{3a} \\ n&=&6 s_2^2+6 s_2+1+(6 s_2+1)(m_2-1)\tag{3b} \\ n&=&6 s_3^2-2 s_3+(6 s_3-1)(m_3-1)\tag{3c}\\ n&=&6 s_4^2+2 s_4+(6 s_4+1)(m_4-1)\tag{3d} \end{eqnarray}$$

$$\begin{equation}n=1,2,3\cdots\end{equation}$$

Give the same integer $n$ to these four equations ( $3$). When there is no integer solution for $s$ and $m$, a twin prime is born from the integer $n$.

When there are no integer solutions in $s$ and $m$, $n$ in equation ( $3$) is written as $n_t$. Using $n_t$, twin primes are given by equation ( $4$).

$$\begin{equation} {\rm Twin\ prime}= \left \{ \begin{array}{l} 6n_t-1 \\ 6n_t+1 \end{array} \right.\tag{4} \end{equation} $$

$$\begin{equation}n_t: {\rm In\ Equation\ (3),{\it n}\ when\ there\ is\ no\ integer\ solution\ for\ {\it s}\ and\ {\it m}.}\end{equation}$$

The following program inputs $n$ and $r$ and searches for a set of twin primes that satisfy the specified "${\rm interval} $". Note that "${\rm interval} $"$=6r-2$ from equation ( $2$).

n =    1;
r = 2;

Clear[nt1, nt2, nt3, pm1, pp1, pm2, pp2, pmr, ppr, intr, int1, int2];
n1 = n;
n2 = n + 1;
nr = n + r;
If[n > 0 && IntegerQ[n] && r > 0 && IntegerQ[r],
  Do[
   Do[func[n1];
    If[func[n1] == {{}, {}, {}, {}}, nt1 = n1, nt1 = 0]
     If[func[n1] == {{}, {}, {}, {}}, Break[]], {n1, n1, n1 + 100}];

   Do[func[n2];
    If[func[n2] == {{}, {}, {}, {}}, nt2 = n2, nt2 = 0]
     If[func[n2] == {{}, {}, {}, {}}, Break[]], {n2, n2, n2 + 100}];

   Do[func[nr];
    If[func[nr] == {{}, {}, {}, {}}, nt3 = nr, nt3 = 0]
     If[func[nr] == {{}, {}, {}, {}}, Break[]], {nr, nr, nr + 100}];

   pm1 = 6*nt1 - 1;
   pp1 = 6*nt1 + 1;
   pm2 = 6*nt2 - 1;
   pp2 = 6*nt2 + 1;
   pmr = 6*nr - 1;
   ppr = 6*nr + 1;
   intr = 6*r - 2;
   int1 = pm2 - pp1;
   int2 = pmr - pp1;

   n1 = n;
   n2 = n + 1;
   nr = n + r;
   If[int1 == intr && int2 == intr, Break[]], {n, n, n + 100}];

  Print["====== The calculation results are shown below. ======"];
  Print["n= ", n];
  Print["r= ", r];
  Print["Specified interval(6*r-2)= ", intr];
  If[int1 == intr && int2 == intr && nt1 > 0, 
   Print["n selected= ", nt1], Print["n selected= -- "]];

  If[int1 == intr && int2 == intr && nt1 > 0, 
   Print["Twin prime(1)= ", {6*nt1 - 1, 6*nt1 + 1}], 
   Print["Twin prime(1)= There are no twin primes in the interval,at \
(n)~(n+100)."]];
  If[int1 == intr && int2 == intr && nt2 > 0, 
   Print["Twin prime(2)= ", {6*nt2 - 1, 6*nt2 + 1}], 
   Print["Twin prime(2)= There are no twin primes in the interval,at \
(n)~(n+100)."]];

  If[int1 == intr && int2 == intr && nt1 > 0 && nt2 > 0, 
   Print["interval(pm2-pp1)= ", int1], "interval(pm2-pp1)= --"];

  If[int1 == intr && int2 == intr && nt1 > 0 && nt2 > 0, 
   Print["PrimeQ[(1),(2)]= ", {{PrimeQ[6*nt1 - 1], 
      PrimeQ[6*nt1 + 1]}, {PrimeQ[6*nt2 - 1], PrimeQ[6*nt2 + 1]}}], 
   Print["PrimeQ[(1),(2)]= {{--,--},{--,--}} "]];

  If[int1 == intr && int2 == intr && nt1 > 0 && nt2 > 0, 
   Print["If you want to find the next twin prime, start with n= ", 
    nt1 + 1], 
   Print["If you want to continue, start with n= ", n + 101]], 
  Print["***** ! Please enter a positive integer. *****"]];

"********************************************************";
func[n_] := 
 Module[{dat1, dat2, dat3, dat4}, 
  dat1 = FindInstance[
    6*s1^2 + (6*s1 - 1)*(m1 - 1) == n && 0 < s1 && 0 < m1, {s1, m1}, 
    Integers]; 
  dat2 = FindInstance[
    6*s2^2 + 6*s2 + 1 + (6*s2 + 1)*(m2 - 1) == n && 0 < s2 && 
     0 < m2, {s2, m2}, Integers]; 
  dat3 = FindInstance[
    6*s3^2 - 2*s3 + (6*s3 - 1)*(m3 - 1) == n && 0 < s3 && 0 < m3, {s3,
      m3}, Integers]; 
  dat4 = FindInstance[
    6*s4^2 + 2*s4 + (6*s4 + 1)*(m4 - 1) == n && 0 < s4 && 0 < m4, {s4,
      m4}, Integers]; {dat1, dat2, dat3, dat4}]
"********************************************************";

This is an example where $n=1$ and $r=2$. Since "${\rm interval} $"$=6r-2=10$. The calculation result is as follows.

====== The calculation results are shown below. ======
n= 1
r= 2
Specified interval(6*r-2)= 10
n selected= 3
Twin prime(1)= {17,19}
Twin prime(2)= {29,31}
interval(pm2-pp1)= 10
PrimeQ[(1),(2)]= {{True,True},{True,True}}
If you want to find the next twin prime, start with n= 4

The calculation result shows the input values $n=1$ and $r=2$. It shows that $r=2$ to ${\rm Specified\ interval} \;(6r-2) = 10$. The search starts from $n=1$ and the solution is found with $n\; {\rm selected} = 3$. This shows that the two twin primes obtained as a solution are ${\rm Twin \,prime}\; (1) = \{17,19\}$ and ${\rm Twin \,prime}\; (2) = \{29,31\}$. It is judged by ${\rm PrimeQ}\; [(1), (2)]$ that the four numbers are indeed prime numbers. Finally, it indicates the next $n$ to start when continuing the search. One search interval is in the range of $n$ to ( $n+100$). If no solution is obtained within the interval, $n$ for searching beyond is also displayed here.

If $r=1$ here, "${\rm interval} $" $= 4$. In this case, it will be the same as $" Search \;for \;consecutive \;twin \;primes "$ described in the previous report.

In writing this program, I used ${\rm Module}\; []$ and ${\rm func} [n {\text _}]: =$ for the first time. Thanks to Claudio-san and William-san for teaching us.

The following table shows two calculation examples. ${\rm Table} \,1$ is an example of $r = 1$, ie "${\rm interval} $" $= 6r-2 = 4$, and ${\rm Table} \,2$ is an example of $r = 5$, ie "${\rm interval} $"$ = 6r-2 = 28$. In both cases, the search was started from $n=1$, and $50$ sets of the selected $n$ and the two pairs of twin primes that were the solutions were recorded.

.

$${\rm Table}\;1\;\; r=2 \;{\rm ( Interval}=10 \ )$$ \begin{array}{|c|c|c|} \hline n\;(r=2)& {\rm Twin \ prime\ (1)}&{\rm Twin \ prime \ (2)}\\ \hline 3 & \text{{17,19}} & \text{{29,31}} \\ 5 & \text{{29,31}} & \text{{29,31}}\\ 10 & \text{{59,61}} & \text{{71,73}}\\ 23 & \text{{137,139}} & \text{{149,151}}\\ 30 & \text{{179,181}} & \text{{191,193}}\\ 38 & \text{{227,229}} & \text{{239,241}}\\ 45 & \text{{269,271}} & \text{{281,283}}\\ 70 & \text{{419,421}} & \text{{431,433}}\\ 135 & \text{{809,811}} & \text{{821,823}}\\ 170 & \text{{1019,1021}} & \text{{1031,1033}}\\ 175 & \text{{1049,1051}} & \text{{1061,1063}}\\ 213 & \text{{1277,1279}} & \text{{1289,1291}}\\ 215 & \text{{1289,1291}} & \text{{1301,1303}}\\ 268 & \text{{1607,1609}} & \text{{1619,1621}}\\ 355 & \text{{2129,2131}} & \text{{2141,2143}}\\ 465 & \text{{2789,2791}} & \text{{2801,2803}}\\ 560 & \text{{3359,3361}} & \text{{3371,3373}}\\ 588 & \text{{3527,3529}} & \text{{3539,3541}}\\ 703 & \text{{4217,4219}} & \text{{4229,4231}}\\ 705 & \text{{4229,4231}} & \text{{4241,4243}}\\ 710 & \text{{4259,4261}} & \text{{4271,4273}}\\ 773 & \text{{4637,4639}} & \text{{4649,4651}}\\ 798 & \text{{4787,4789}} & \text{{4799,4801}}\\ 835 & \text{{5009,5011}} & \text{{5021,5023}}\\ 940 & \text{{5639,5641}} & \text{{5651,5653}}\\ 978 & \text{{5867,5869}} & \text{{5879,5881}}\\ 1115 & \text{{6689,6691}} & \text{{6701,6703}}\\ 1130 & \text{{6779,6781}} & \text{{6791,6793}}\\ 1158 & \text{{6947,6949}} & \text{{6959,6961}}\\ 1258 & \text{{7547,7549}} & \text{{7559,7561}}\\ 1370 & \text{{8219,8221}} & \text{{8231,8233}}\\ 1500 & \text{{8999,9001}} & \text{{9011,9013}}\\ 1570 & \text{{9419,9421}} & \text{{9431,9433}}\\ 1843 & \text{{11057,11059}} & \text{{11069,11071}}\\ 1860 & \text{{11159,11161}} & \text{{11171,11173}}\\ 2040 & \text{{12239,12241}} & \text{{12251,12253}}\\ 2280 & \text{{13679,13681}} & \text{{13691,13693}}\\ 2285 & \text{{13709,13711}} & \text{{13721,13723}}\\ 2333 & \text{{13997,13999}} & \text{{14009,14011}}\\ 2425 & \text{{14549,14551}} & \text{{14561,14563}}\\ 2985 & \text{{17909,17911}} & \text{{17921,17923}}\\ 3008 & \text{{18047,18049}} & \text{{18059,18061}}\\ 3020 & \text{{18119,18121}} & \text{{18131,18133}}\\ 3598 & \text{{21587,21589}} & \text{{21599,21601}}\\ 3600 & \text{{21599,21601}} & \text{{21611,21613}}\\ 3838 & \text{{23027,23029}} & \text{{23039,23041}}\\ 4375 & \text{{26249,26251}} & \text{{26261,26263}}\\ 4450 & \text{{26699,26701}} & \text{{26711,26713}}\\ 4480 & \text{{26879,26881}} & \text{{26891,26893}}\\ 4588 & \text{{27527,27529}} & \text{{27539,27541}}\\
\text{Omitted below} & \text{Omitted below} &\text{Omitted below}\\ \hline \end{array}

. $${\rm Table}\;2\;\; r=5 \;{\rm ( Interval}=28 \ )$$ \begin{array}{|c|c|c|} \hline n\;(r=5)& {\rm Twin \ prime\ (1)}&{\rm Twin \ prime \ (2)}\\ \hline 12 & \text{{71,73}} & \text{{101,103}}\\ 18 & \text{{107,109}} & \text{{137,139}}\\ 25 & \text{{149,151}} & \text{{179,181}}\\ 33 & \text{{197,199}} & \text{{227,229}}\\ 40 & \text{{239,241}} & \text{{269,271}}\\ 47 & \text{{281,283}} & \text{{311,313}}\\ 72 & \text{{431,433}} & \text{{461,463}}\\ 95 & \text{{569,571}} & \text{{599,601}}\\ 138 & \text{{827,829}} & \text{{857,859}}\\ 177 & \text{{1061,1063}} & \text{{1091,1093}}\\ 242 & \text{{1451,1453}} & \text{{1481,1483}}\\ 278 & \text{{1667,1669}} & \text{{1697,1699}}\\ 333 & \text{{1997,1999}} & \text{{2027,2029}}\\ 373 & \text{{2237,2239}} & \text{{2267,2269}}\\ 385 & \text{{2309,2311}} & \text{{2339,2341}}\\ 443 & \text{{2657,2659}} & \text{{2687,2689}}\\ 495 & \text{{2969,2971}} & \text{{2999,3001}}\\ 550 & \text{{3299,3301}} & \text{{3329,3331}}\\ 555 & \text{{3329,3331}} & \text{{3359,3361}}\\ 637 & \text{{3821,3823}} & \text{{3851,3853}}\\ 670 & \text{{4019,4021}} & \text{{4049,4051}}\\ 688 & \text{{4127,4129}} & \text{{4157,4159}}\\ 753 & \text{{4517,4519}} & \text{{4547,4549}}\\ 1045 & \text{{6269,6271}} & \text{{6299,6301}}\\ 1110 & \text{{6659,6661}} & \text{{6689,6691}}\\ 1243 & \text{{7457,7459}} & \text{{7487,7489}}\\ 1260 & \text{{7559,7561}} & \text{{7589,7591}}\\ 1433 & \text{{8597,8599}} & \text{{8627,8629}}\\ 1495 & \text{{8969,8971}} & \text{{8999,9001}}\\ 1502 & \text{{9011,9013}} & \text{{9041,9043}}\\ 1668 & \text{{10007,10009}} & \text{{10037,10039}}\\ 1673 & \text{{10037,10039}} & \text{{10067,10069}}\\ 1712 & \text{{10271,10273}} & \text{{10301,10303}}\\ 1717 & \text{{10301,10303}} & \text{{10331,10333}}\\ 1738 & \text{{10427,10429}} & \text{{10457,10459}}\\ 1750 & \text{{10499,10501}} & \text{{10529,10531}}\\ 1810 & \text{{10859,10861}} & \text{{10889,10891}}\\ 1990 & \text{{11939,11941}} & \text{{11969,11971}}\\ 2007 & \text{{12041,12043}} & \text{{12071,12073}}\\ 2317 & \text{{13901,13903}} & \text{{13931,13933}}\\ 2427 & \text{{14561,14563}} & \text{{14591,14593}}\\ 2555 & \text{{15329,15331}} & \text{{15359,15361}}\\ 2898 & \text{{17387,17389}} & \text{{17417,17419}}\\ 2993 & \text{{17957,17959}} & \text{{17987,17989}}\\ 3197 & \text{{19181,19183}} & \text{{19211,19213}}\\ 3327 & \text{{19961,19963}} & \text{{19991,19993}}\\ 3332 & \text{{19991,19993}} & \text{{20021,20023}}\\ 3413 & \text{{20477,20479}} & \text{{20507,20509}}\\ 3453 & \text{{20717,20719}} & \text{{20747,20749}}\\ 3497 & \text{{20981,20983}} & \text{{21011,21013}}\\
\text{Omitted below} & \text{Omitted below} &\text{Omitted below}\\ \hline \end{array}