How To: Calculate All Derivatives

Mat = Outer[Coefficient,
    D[Dot[{1, D[-4 x (1 - x), x], -4 x (1 - x)},
        {T[x], D[T[x], x], D[T[x], {x, 2}]}],
       {x, #}] & /@ Range[0, 10], D[T[x],
       {x, #}] & /@ Range[0, 11]] /. x -> 0;
Prepend[Mat, Prepend[Table[0, 11], 1]] // MatrixForm
LinearSolve[Prepend[Mat, Prepend[Table[0, 11], 1]], 
 Prepend[Table[0, 11], 1]]

And notice, this acutally requires only one initial condition, not even two!

How To: DIY NDSolve

DerMat[n_] := Join[
   IdentityMatrix[n + 3][[1 ;; 2]],
   Outer[Coefficient,
    D[Dot[{1, D[-4 x (1 - x), x], -4 x (1 - x)},
        {T[x], D[T[x], x], D[T[x], {x, 2}]}],
       {x, #}] & /@ Range[0, n], D[T[x],
       {x, #}] & /@ Range[0, n + 2]]];

GetNext[mat_, cond_, dx_] := With[{Tx = Dot[
     LinearSolve[mat /. x -> cond[[3]], Join[cond[[1 ;; 2]],
       Table[0, Length[mat] - 2]]], 
     1/#! x^# & /@ Range[0, Length[mat] - 1]]
   }, {Tx, D[Tx, x], cond[[3]] + dx} /. x -> dx]

AbsoluteTiming[
 FApprox = Function[{MAT},
        Interpolation[
         NestList[GetNext[MAT, #, .0001] &, {1, 1/4, 0}, 
           9999][[All, {3, 1}]]]][DerMat[#]] & /@ {2, 3, 4, 5, 6} // 
    Quiet;]

Show[LogPlot[
    Abs[FApprox[[#]][x] - 2/Pi EllipticK[x]], {x, .001, .9999}, 
    PlotRange -> All, 
    PlotStyle -> {Red, Orange, Yellow, Green, Blue}[[#]]] & /@ 
  Range[5],
 LogPlot[10^(-#), {x, 0, 1}, PlotStyle -> Black] & /@ {7, 11},
 PlotRange -> All]

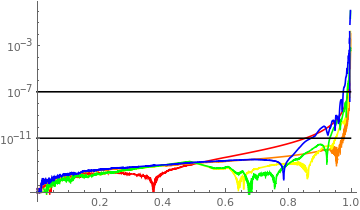
Compare with earlier error plot. This quick hack is already doing better than NDSolve, and accepts initial condition at x=0. Any thoughts?

Your differential equation is of the second order, but you give three initial data. Also, at the the starting point x==0 of the equation is singular:

NDSolve[{T[x] + 4 (-1 + 2 x) Derivative[1][T][x] + 
    4 (-1 + x) x (T^\[Prime]\[Prime])[x] == 0, T[0] == 1, 
  T'[0] == 1/4, T''[0] == 9/32}, T, {x,
   0, 1}]

DSolve gives a solution, which is probably equivalent with yours:

DSolve[Prepend[ICs, Eq1], T, x]