Michael,
The only thing that matters is that t/tau is an integer. It does not matter to the answer if t=7 tau or if t = 5 tau. The answer is the same as long as N is larger than 7 (in this case). This is precisely what MMA is saying: if t<=N tau it means that the summation must include the situation where t = n*tau during the summation. The best way to convince yourself it is correct is try some numerical values.
Grid[Prepend[
Table[{t, t/\[Tau], t1} /. N -> 10 /. \[Tau] -> 1, {t, 1, 15,
1}], {"t", "t/\[Tau]", "t1"}], Background -> {None, {LightGray}},
Frame -> All]
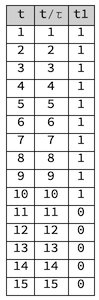
Now change numbers, for example:
Grid[Prepend[
Table[{t, t/\[Tau], t1} /. N -> 10 /. \[Tau] -> 1.1, {t, 1,
15}], {"t", "t/\[Tau]", "t1"}], Background -> {None, {LightGray}},
Frame -> All]
to get
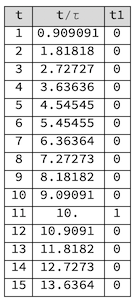
I hope this is clear.
Regards
Neil