Group Abstract Group Abstract

Message Boards Message Boards

Simplify sum expression containing Kronecker delta?

Michael Helmle
Posted 6 years ago

Hello Community,

I tried to formulate an expression that contains a sum over KroneckerDeltafunctions. 

 te[x] + v[x] \[Tau]   \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = 0\), \(N\)]\(KroneckerDelta[t, 
     n\ \[Tau]]\)\), 
 N > 0 && t >= 0 & \[Tau] >= 0 && {n, N} \[Element] 
   Integers && {x , t, \[Tau]} \[Element] Reals]

Using Simplify and FullSimplify with the appropiate conditions on the Integer and Real variables I get the following result:

t1 = FullSimplify[ te[x] + v[x] \[Tau]   \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = 0\), \(N\)]\(KroneckerDelta[t, 
      n\ \[Tau]]\)\), 
  N > 0 && t >= 0 & \[Tau] >= 0 && {n, N} \[Element] 
    Integers && {x , t, \[Tau]} \[Element] Reals]

enter image description here

Apparently Mathematica has not considered all of the constraints like N >0 etc. Any ideas on how to improve the output of this calculation?
POSTED BY: Michael Helmle
8 Replies
Sort By:
Michael Helmle
Michael Helmle
Posted 6 years ago

Hello Neil,

You are complete right, this is the point which I did not understand in the beginning. The expression "1 - Ceiling ... + Floor" encodes not for one condition, but for many. This way the sum of KroneckerDeltas (each of these represents one condition) can be absorbed into one expression.

Thank you very much for explanations and enlighten me,

All the best,

Michael
POSTED BY: Michael Helmle

Michael,

The only thing that matters is that t/tau is an integer. It does not matter to the answer if t=7 tau or if t = 5 tau. The answer is the same as long as N is larger than 7 (in this case). This is precisely what MMA is saying: if t<=N tau it means that the summation must include the situation where t = n*tau during the summation. The best way to convince yourself it is correct is try some numerical values.

Grid[Prepend[
  Table[{t, t/\[Tau], t1} /. N -> 10  /. \[Tau] -> 1, {t, 1, 15, 
    1}], {"t", "t/\[Tau]", "t1"}], Background -> {None, {LightGray}}, 
 Frame -> All]

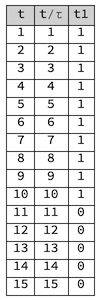
enter image description here

Now change numbers, for example:

Grid[Prepend[
  Table[{t, t/\[Tau], t1} /. N -> 10  /. \[Tau] -> 1.1, {t, 1, 
    15}], {"t", "t/\[Tau]", "t1"}], Background -> {None, {LightGray}},
  Frame -> All]

to get

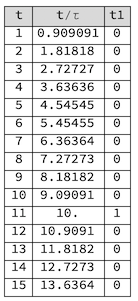
enter image description here

I hope this is clear.

Regards

Neil
POSTED BY: Neil Singer
Michael Helmle
Michael Helmle
Posted 6 years ago
POSTED BY: Michael Helmle

Michael,

I think Mathematica is correct. If you have KroneckerDelta[t, n tau], if you sum to a number N equal to or larger than 7, you will have:

 KroneckerDelta[t, 0 tau] + KroneckerDelta[t, 1 tau]+... + KroneckerDelta[t, 7 tau]+  KroneckerDelta[t, 8 tau]+...

since only KroneckerDelta[t, 7 tau] is 1 and the rest are zero, your sum is 1. If t is not an integer multiple of tau then you will never get a 1.

Regards,

Neil
POSTED BY: Neil Singer
Michael Helmle
Michael Helmle
Posted 6 years ago
POSTED BY: Michael Helmle
POSTED BY: Neil Singer
Michael Helmle
Michael Helmle
Posted 6 years ago

Hello Neil,

Thank you for pointing this out, this was definitely a typo. The expression look smuch better now. I changed the condition slightly ( tau >0 instead of tau >= 0).

Assuming[{N > 0 && t >= 0 && \[Tau] > 0 && {n, N} \[Element] 
            Integers && {x , t, \[Tau]} \[Element] Reals}, 
  FullSimplify[ te[x] + v[x] \[Tau]   \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = 0\), \(N\)]\(KroneckerDelta[t, 
      n\ \[Tau]]\)\)]]

As result I get now: enter image description here

But something still puzzles me: I would expect to get n-times this expression. For example, put N=3, I would expect that the 4 KroneckerDeltas will add up to 4 times this expression with corresponding arguments for Ceiling, Floor, respectively, t/tau = { t/0, t/tau, t/( 2tau), t/(3 tau). Where do I go wrong here?
POSTED BY: Michael Helmle

Michael,

You have a typo (I think). Your second & should be &&

N > 0 && t >= 0 && \[Tau] >= 0 && {n, N} \[Element] 
    Integers && {x , t, \[Tau]} \[Element] Reals

Now it can simplify. You can also do:

Assuming[{N > 0 && t >= 0 && \[Tau] >= 0 && {n, N} \[Element] 
        Integers && {x , t, \[Tau]} \[Element] Reals}, 
 FullSimplify[ te[x] + v[x] \[Tau]   \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = 0\), \(N\)]\(KroneckerDelta[t, 
      n\ \[Tau]]\)\)]]

Regards,

Neil
POSTED BY: Neil Singer
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard