Not sure how your code actually produced a result since it produced some errors for me.
NIntegrate only works when the boundaries are numerical. Therefore when you use it as a fit function you have to be sure the function only evaluates if the input parameters are numerical.
You can use the same function for your data generation and your fitting.
Also with minimization problems the initial fit value should be close to the expected values since you are using local minimization "LevenbergMarquardt". Therefore give initial values close to the expected values.
fm[x_, y_, t_, b_, l_, d_] /;
NumberQ[x] && NumberQ[b] && NumberQ[l] && NumberQ[d] :=
Intens/(2*\[Pi]*K0)*
NIntegrate[
Sqrt[1 + m1^2]*
Erfc[Sqrt[(x - \[Alpha])^2 + (y - \[Beta])^2 + (z - (m1*\[Alpha] -
d))^2]/
Sqrt[Dif*4*
t]]/(Sqrt[(x - \[Alpha])^2 + (y - \[Beta])^2 + (z - (m1*\
\[Alpha] - d))^2]), {\[Beta], -b/2, b/2}, {\[Alpha], linf\[Alpha],
l*lsup1}]
Block[{y = 0, t = 1, b = 0.0015, l = 0.0011, d = 0.00013},
data = Table[{x,
fm[x, y, t, b, l, d] +
Random[NormalDistribution[0, 0.1]]}, {x, -0.0015, 0.002,
0.000015}]
];
fit = FindFit[data,
fm[x, 0, 1, b, l, d], {{b, 10.^-3}, {l, 10.^-3}, {d, 10.^-4}}, x,
Method -> "LevenbergMarquardt"]
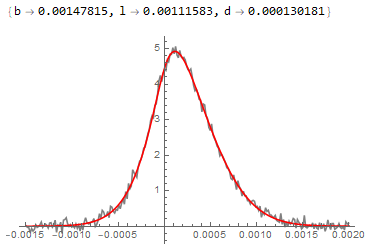
Show[ListLinePlot[data, PlotStyle -> Gray, PlotRange -> All],
Plot[fm[x, 0, 1, b, l, d] /. fit, {x, -0.0015, 0.002},
PlotStyle -> Red]]
Or switch to a global optimizer "NMinimize" which will probably also do the job but is much slower and has the risk of going to regions where your function is ill defined.