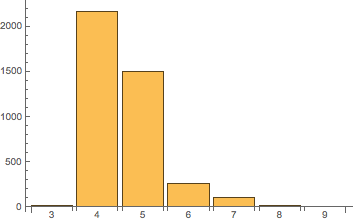IGraph/M now has its own DOI, and you can find citation information here: https://doi.org/10.5281/zenodo.1134932 There is a "cite as" box on the right hand side, a bit down on the page.

I made a new release of IGraph/M which fixes the error checking in IGImport. Now it should not blow up if it gets unexpected input.

GraphData is just a database a curated collection of graphs. As I remember, it is exhaustive up to 7 vertices, but above that, it only includes examples of special interest.

Do not use GraphData if you want all graphs with a certain property (at least not above $n=7$).

To generate all cubic graphs, I recommend the geng tool from the nauty suite. You will need to compile and install these tools on your own (unless your operating systems package manager has them; I usually get them with MacPorts).

geng outputs graphs in Graph6 format, which Mathematica's built-in Import can read, but IGImport in the IGraph/M package can read even faster. (IGraph/M also supports importing directed graphs in this format—Import currently does not.)

Get IGraph/M here: http://szhorvat.net/mathematica/IGraphM

Here's an example that counts how many cubic graphs are there on 12 vertices with different diameters:

IGImport["!geng -d3 -D3 12", "Nauty"] // Map[IGDiameter] // Counts // KeySort

(* <|3 -> 34, 4 -> 43, 5 -> 6, 6 -> 2, \[Infinity] -> 9|> *)

There are 34 with diameter 3, 43 with 4, etc. A diameter of Infinity means that the graph is disconnected.

-d3 -D3 in the geng call sets both the minimum and the maximum degree to 3. If you are not interested in disconnected graphs, we can filter those with -c.

Now we can go to bigger graphs: this only takes 1.5 seconds on my machine.

IGImport["!geng -d3 -D3 -c 16", "Nauty"] // Map[IGDiameter] // Counts // KeySort

(* <|3 -> 14, 4 -> 2167, 5 -> 1499, 6 -> 261, 7 -> 101, 8 -> 14, 9 -> 4|> *)

BarChart[%, ChartLabels -> Automatic]