Playing cards + Mathematica + Numberphile + PS4 = quarantine starter pack
Abstract
In this episode Brady shares his favorite number with Matt and memorizes a chosen card from 27-card deck without telling Matt. Matt asks Brady same question for three times to locate the chosen card precisely at the position indicated by Brad's favorite number with modular algorithm and ternary number system.
The code in the notebook may be a little lengthy and I do not want to skip any all critical intermediate stages in this step by step walkthrough just like the Numberphile video. You can download all input codes at the end of this article.
Play the Game
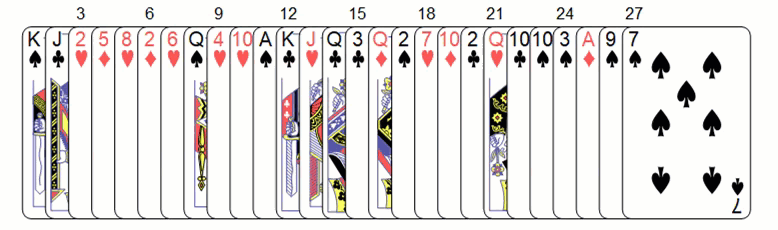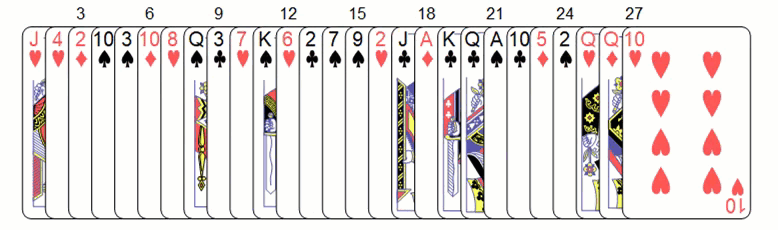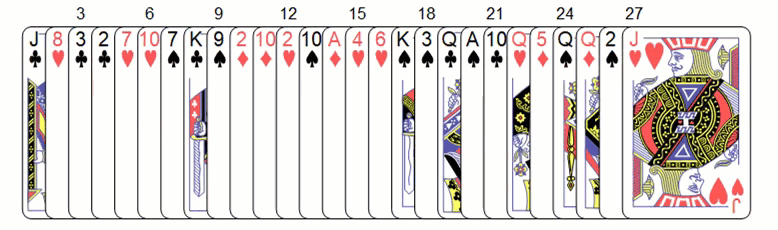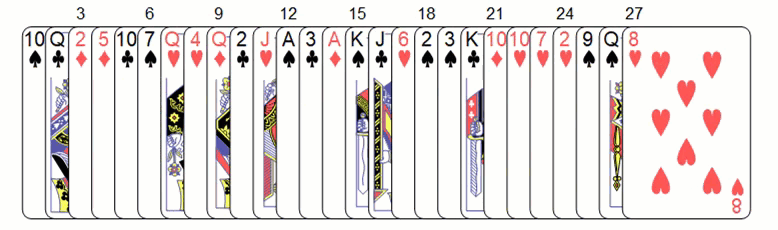
Matt draws a random deck of 27 playing cards from a standard pack of 52 cards (joker cards discarded). Set a seed for random generation so we can use the same data again.
SeedRandom[4321];
deck = RandomSample[Range[52], 27];
(* {23,41,1,19,28,52,13,31,7,51,12,27 ... } *)
Each code above corresponds to a playing card with its suits sorted in the following way
- 01 - 13: Ace to King/Spades
- 14 - 26: Ace to King/Heart
- 27 - 39: Ace to King/Diamonds
- 40 - 52: Ace to King/Clubs
We can display the deck with the following function from Wolfram Function Repository

I also define the showFullDeck function based on ResourceFunction["PlayingCardGraphic"]. This function returns a Graphics object, therefore most options is implicitly inherited from Graphics. I added several options to control the output size, the arrangement of cards and numbered labels. The second argument controls whether I need to add a tag to highlight a card in the deck. If no value is given, the default value is zero. The logic in the Epilog will not create a circular tag. Otherwise, the circular tag is added at the card we choose. Because I know each card is unique, I just take the first row and first column from a Position function call
showFullDeck[deck_,num_:0]:=ResourceFunction["PlayingCardGraphic"][deck,
"CardSpreadAngle"->0,"CardOffset"-> {0.45,0},ImageSize->{440,145},
Epilog->{If[num==0,Nothing,
Style[ Circle[{-1+0.45 * Position[deck,num][[1,1]],1.45},{0.25,0.45}],Thick,Blue]],
Table[Text[ToString[k],{-1+0.45 * k,2.1}],{k,3,27,3}]}]//Rasterize
I can use this function to show the Matt's hand of deck. The numbers above cards are ordered in such a way that one deals the left most card first as all cards face down.
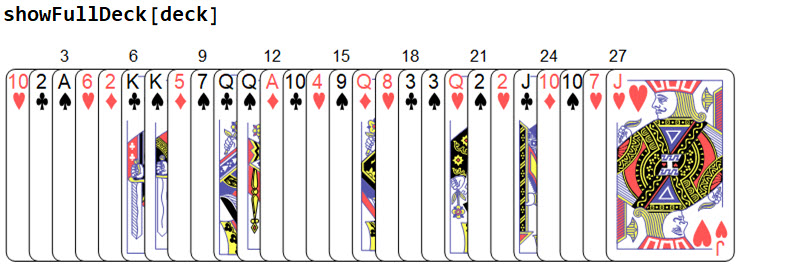
I can make the step-by-step demonstration a little simpler than in video. Matt asks Brady to pick up a number. Brady says it out loudly
favNumber = RandomInteger[{1, 27}]
(* 10 *)
Then Matt immediately makes the following critical calculation in head without telling Brady. First he removes 1 from the number, and converts the decimal number into base 3. Here I need to pad zero to the left of this representation so that once the digits are reversed, I still can get a list of three numbers
rTerDig = Reverse@IntegerDigits[favNumber - 1, 3, 3]
(* {0,0,1} *)
Brady is then asked to pick a secret card from the deck and he only shares the information with audience.
secretCard = RandomChoice[deck]
(* 12 *)
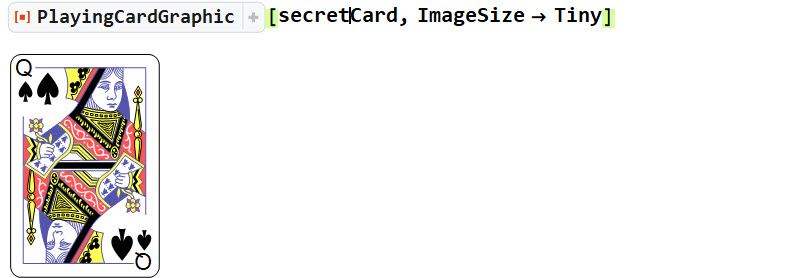
Now Matt is going to deal the deck in this way:
deal3Piles[splittedDeck_,sc_:0]:=Framed[Rasterize@Row@Map[
ResourceFunction[PlayingCardGraphic] [#,
"CardSpreadAngle"->0,"CardOffset"-> {0.15,-0.72},
ImageSize->{100,280},
Epilog->If[MemberQ[#,sc],
Style[Circle[
{0.15 * (Position[#,sc][[1,1]]-7),-0.72*(Position[#,sc][[1,1]]-2)}
,{0.25,0.45}],Blue,Thickness[0.08]],
{}]]&,splittedDeck]]
So the first card goes to left (1st) pile, second card middle, third card right, fourth card first, fifth card middle and so on, until all 27 cards are dealt. Illustrated below. All cards are facing up on the table.
firstDeal = Transpose@Partition[deck, 3, 3];
deal3Piles[firstDeal, secretCard]
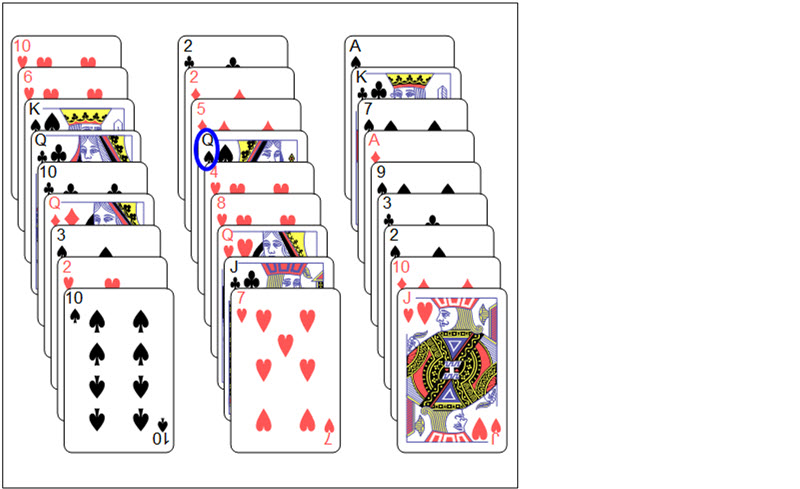
Matt asks Brady to point out which pile contains the chosen card. Brady answers
pile1 = Position[firstDeal, secretCard][[1, 1]]
(* 2 *)
Matt then pile-shuffles the three group by stacking them in this order
shuffle1 = Cases[permute, _?(#[[rTerDig[[1]] + 1]] == pile1 &)][[1]]
(* {2,1,3} *)
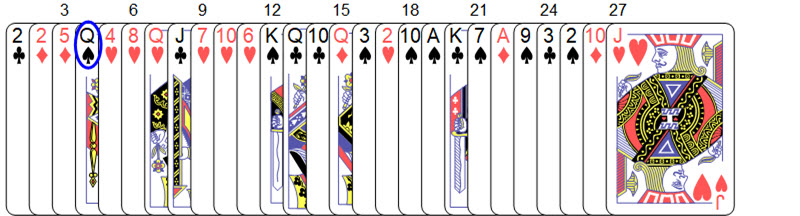
This tuple simply means that when one needs to put three piles into one pile, the middle pile from the diagram should be decked on top of the other two piles, with all cards facing down. Once this is done, the sequence of all cards after this operation is
newDeck = Join @@ firstDeal[[shuffle1]];
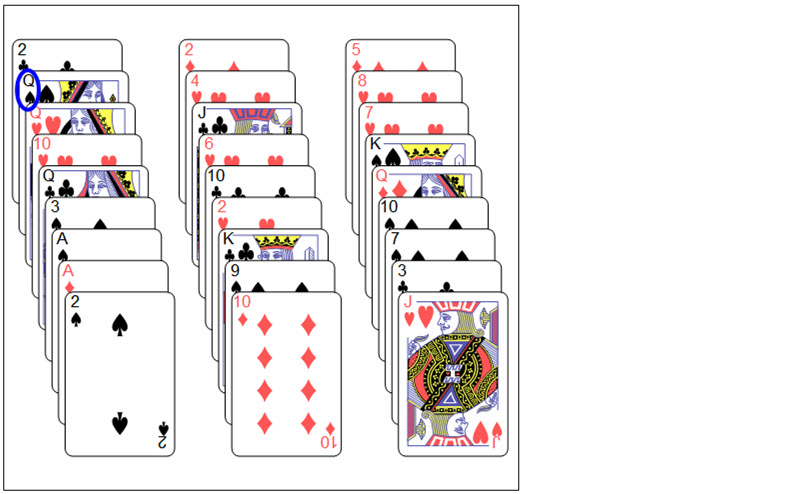
showFullDeck[newDeck, secretCard]
Use the above newly sorted deck and deal to 3 piles likewise
secondDeal = Transpose@Partition[newDeck, 3, 3];
deal3Piles[secondDeal, secretCard]
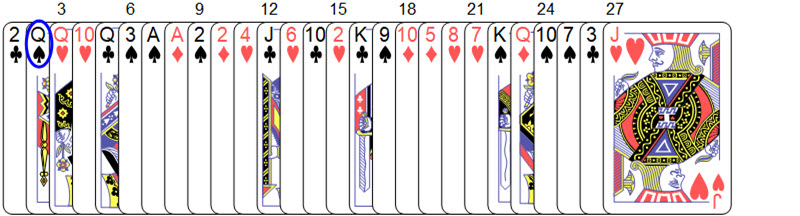
Matt asks Brady the second time to point out the deck containing the secret card
pile2 = Position[secondDeal, secretCard][[1, 1]]
(* 1 *)
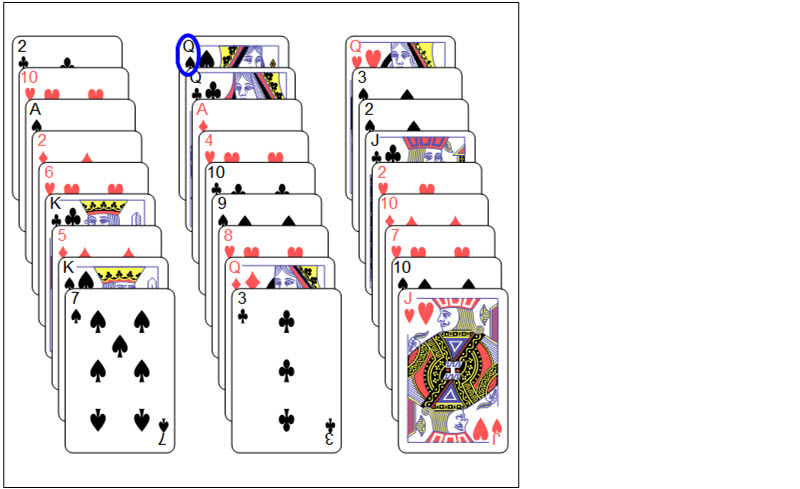
Matt pile-shuffles again and this time the order for Matt's new deck from top to bottom is left, middle and right pile, respectively. Let's take a look at the new deck after shuffle
newDeck = Join @@ secondDeal[[shuffle2]];
showFullDeck[newDeck, secretCard]
Matt deals these cards for the third time and asks Brady the same question again
thirdDeal = Transpose@Partition[newDeck, 3, 3];
deal3Piles[thirdDeal, secretCard]
Brady points out the following pile containing the secret card
pile3 = Position[thirdDeal, secretCard][[1, 1]]
(* 2 *)
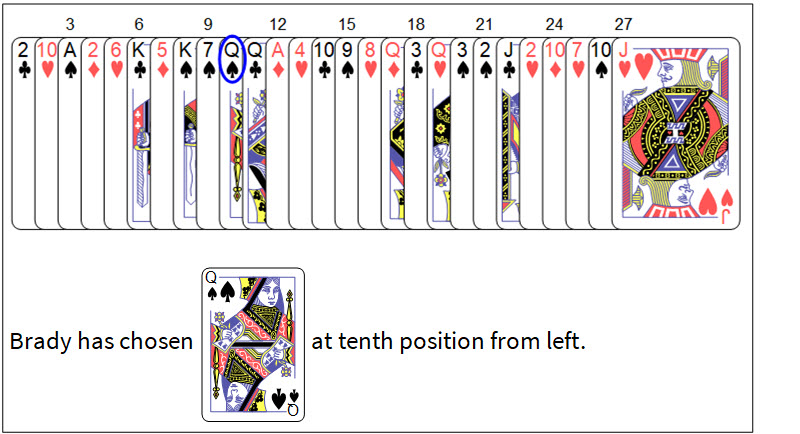
Matt shuffles three piles for the last time the same way before and he concludes that
shuffle3=Cases[permute,_?(#[[rTerDig[[3]]+1]]==pile3&)][[1]];
newDeck=Join@@thirdDeal[[shuffle3]];
Framed[Style[Column[{showFullDeck[newDeck,secretCard],
Row[{"Brady has chosen ",
ResourceFunction["PlayingCardGraphic"][secretCard,ImageSize->64],
" at ",IntegerName[favNumber,{"English","Ordinal"}] ," position from left."}]}],
ImageSizeMultipliers->1,FontFamily->"Source Sans Pro",FontSize->15]]
Remark
- Readers can comment out the starting line with SeedRandom to create your own shuffled deck to begin with. Just find and click Evaluation -> Evaluate Notebook in toolbar to automatically generate games.
- You can find a nice proof from Saha, Teaching the Ternary Base Using a Card Trick
- Gardner, Martin.Mathematics, Magic and Mystery. Dover Publications 1956.
Do not forget to checkout another card trick article in the community inspired by Numberphile.
 Attachments:
Attachments: