MODERATOR NOTE: coronavirus resources & updates: https://wolfr.am/coronavirus

Are the measures taken getting us closer to herd immunity?

In this post I will look at one simple, but very important, aspect of a pandemic, namely herd immunity and what's required to reach it. My ambition is to write something that does not require any mathematical experience and that hopefully leaves you with a positive feeling at the end.

If you already know how exponential growth and herd immunity work, you may skip the first two sections.

Exponential growth - What is R0 and why is it important?

By now, most of you have heard about the R0 ,or basic reproduction number. To understand herd immunity you need to understand this number.

R0 tells you how many people, on average, each infected person will infect. If one person infects two on average, then the number is two. Below you can test a few different values and see how many persons will be infected within four steps (even though not entirely correct, you can think about it as days if you like) depending on R0 number. Select the R0 number and then drag the slider to see how many have been infected at any given point in time.

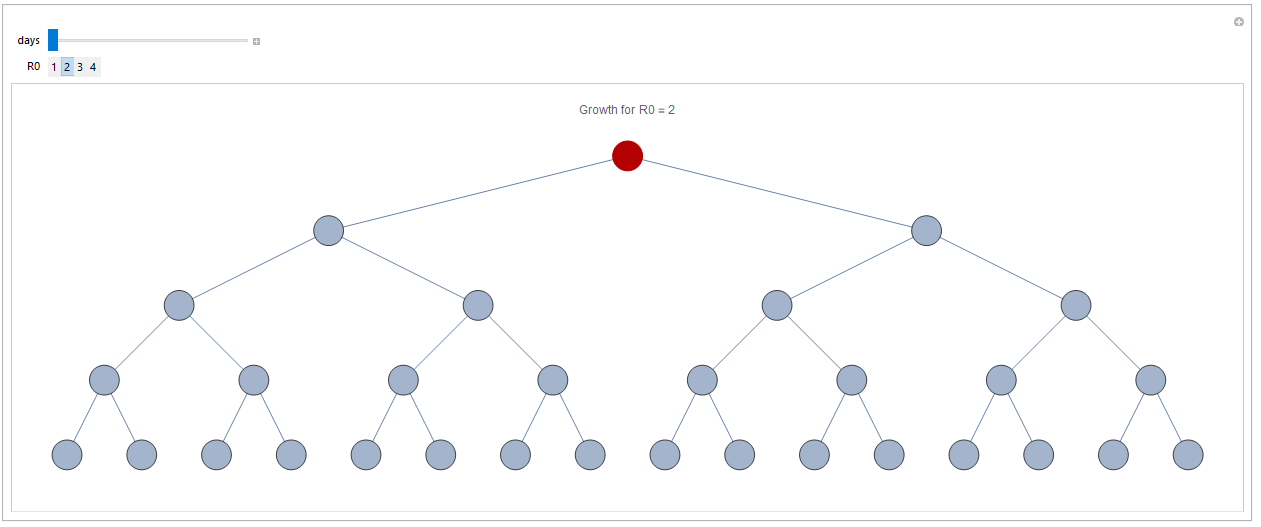
Infection after three days with R0=2:

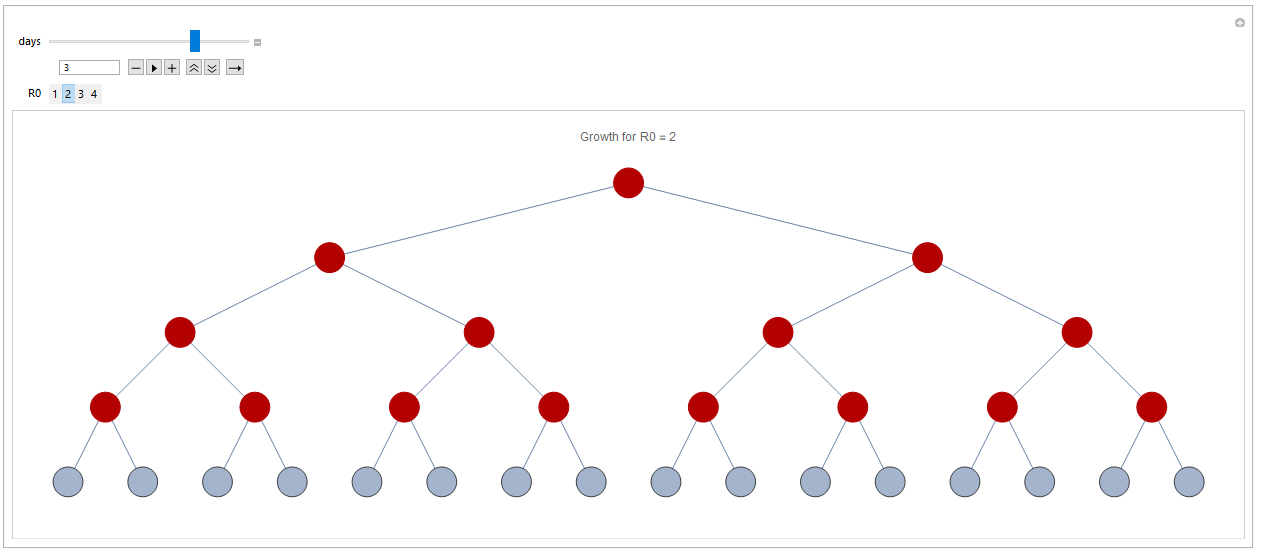
For simplicity I have assumed that it takes one day before an infected person has infected everyone that they will infect. For COVID-19, just as for most it actually takes longer, so this slows down the process somewhat. However, the principle is the same.

COVID-19 is believed to have an R0 number between 1.4 and 3.9 (reference). As you can see the number of infected grows incredibly fast already at the higher range, but a bit more modest at lower.

If we assume no immunity, i.e. people can get sick again and again, then the growth for values between 1 and 4 would look like this:

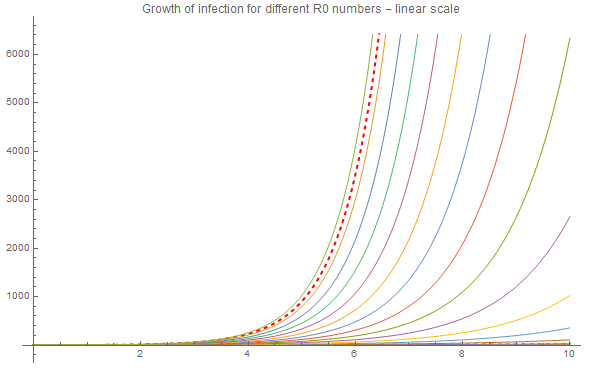
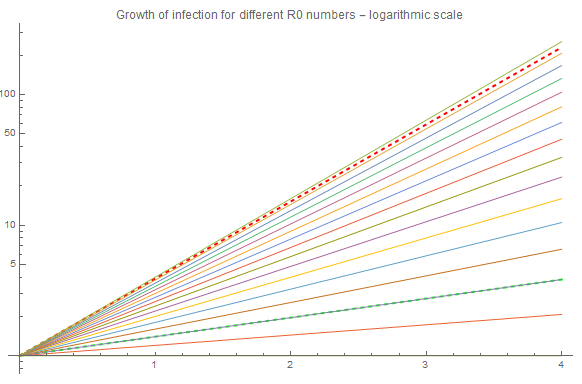
The red dashed curve represents R0 = 3.9, i.e. the upper range of COVID-19, and there is a green dashes representing the lower range, R0 = 1.4. This has a growth rate that is so close to zero, so it is hard to detect it. If we change to a a logarithmic plot it is easier to see:

Immunity - How does immunity impact the epidemic?

Most people that get infected will recover and get immune. Let's look at the case of R0 = 2, with 50% of the population being immune. If you click the immune checkbox every second point will become green, indicating people that are immune. Now, the first infected will only infect one person, meaning that the first immune person is protecting every person on the left side. The first person at the right will be infected, but yet again he will only infect one person.

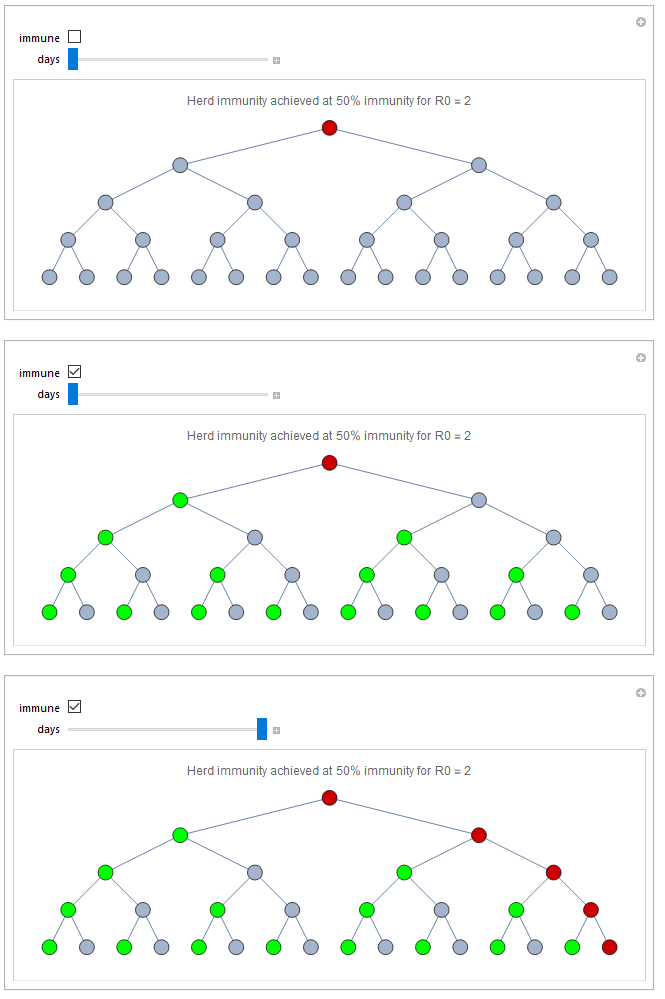
Immunity will not spread equally of course. For instance, instead of the scenario I showed above we could imagine that everyone at the left side is immune and non at the right hand side. The the whole right hand side would be infected after 5 days. On the other hand it is enough that person 2 and 3 are immune to stop the entire disease.

Of course the populations we are talking about are much larger than this example and people are connected in much more advanced network. However, the example above illustrates well the behavior one can expect in this situation. This can be summarized in a very simple equation:

s = 1 / R0

where s is the proportion of the population that is susceptible to the virus. Thus for R0 = 2 gives a threshold of 50%, R0 = 3 gives 33%, and R0 = 4 gives 25%, meaning that 50%, 67%, and 75%, respectively, has to be immune in order to achieve herd immunity. The average estimated R0 for COVID-19 is 2.65 which corresponds to around the 60% immunity that you probably heard epidemiologists talk about.

Current immunity and growth rates

Let us look at the current development in a few countries and how many have been identified as infected this far. I will remove the initial phase, and start from the day that each country reached 100 confirmed cases.

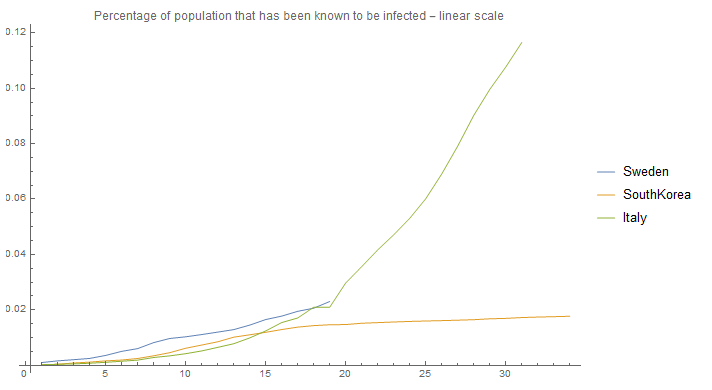
This looks quite different from the graph "Growth of infection for different R0 numbers - linear scale" showed previously, so let's look at the data in a logarithmic scale:

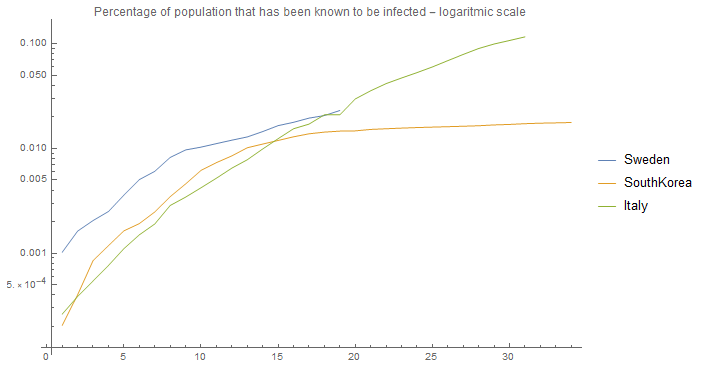
Instead of being straight lines as shown in "Growth of infection for different R0 numbers - logarithmic scale" the lines are flattening out over time. Why?

There are basically two possible solutions

• either the population is getting immune
• or the policies taken are having effects.

The graph, "Percentage of population that has been known to be infected - linear scale" showed that there has been so few cases yet, that there is probably no effect at all from herd immunity. At least assuming that the number of know cases are within one order of magnitude of the actual cases. Therefore the effect that immunity has on this policy dependent R0, let's call it RO^, can be neglected at this stage of the process (if we are lucky though there are a lot of unknown cases, that can help us get to herd immunity faster). Thus, the decrease of RO^ is likely due to policies.

If we take the ratio between each days we will get the current RO^:

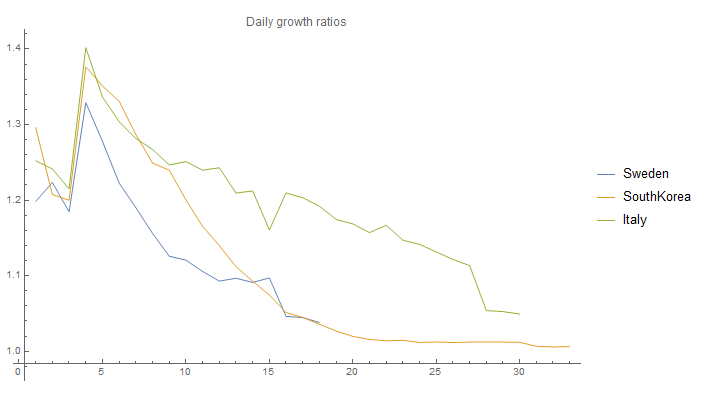
It is obvious that RO^ decreases over time for all three countries. This is actually the case for all countries, except for possibly the US. As seen it is very close to 1 in the case of South Korea, and even Italy is below 1.1!

Herd immunity - and why we are closer to reach it then you think

Remember that herd immunity is achieved when

s = 1 / R0

If we consider the case that each country maintains it's current policies, the herd immunity under those conditions is:

s = 1 / RO^

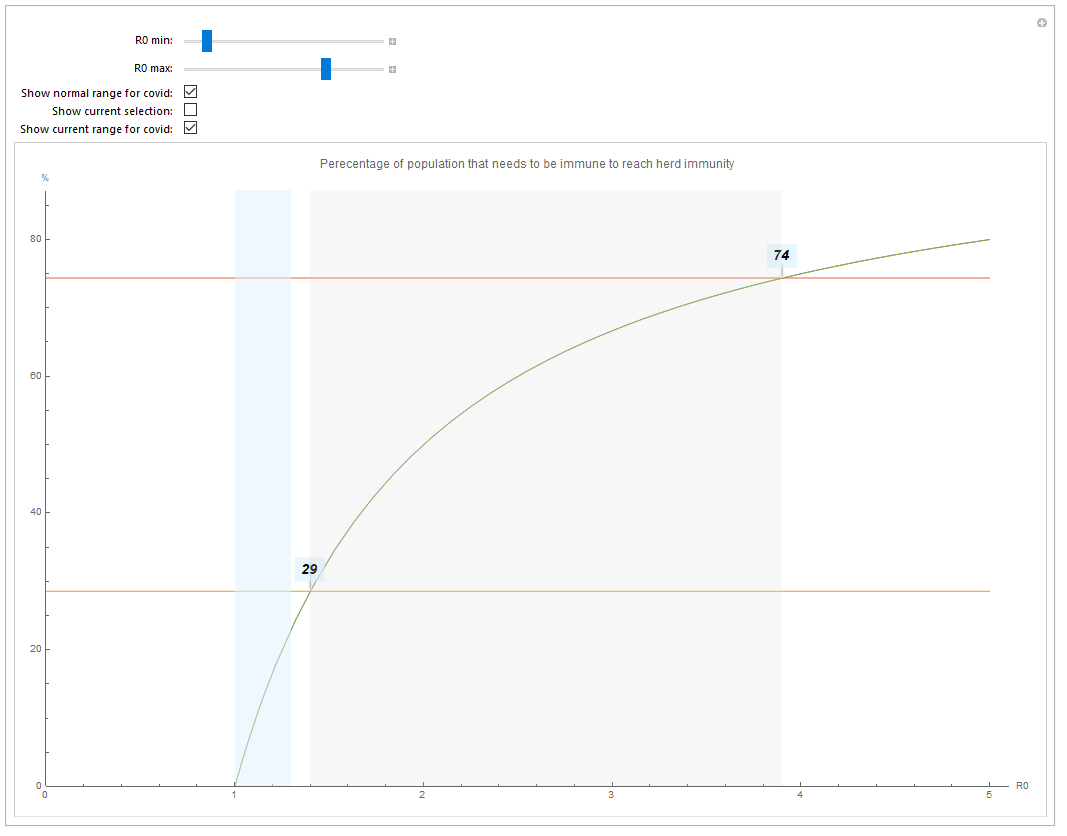
So let us look at which proportion of the population needs to be immune in order to get herd immunity.

• Use R0 min and RO max to set an interval
• The grey zone shows the R0 range (1.4 - 3.9) for COVID-19 according to current studies.
• The orange will highlight your currently selected range (deactivated by default)
• The blue range shows the current RO^ for countries with more than 100 cases (ranging from South Korea and possibly China to the US).
• The horizontal lines show the immunity needed to reach herd immunity (i.e. between 29% - 75% for COVID-19)

Setting R0^ = 1.02 (South Korea's current value) results in only 2% needed for herd immunity, given that the current policies are kept. Sweden's 1.05 corresponds to 5%.

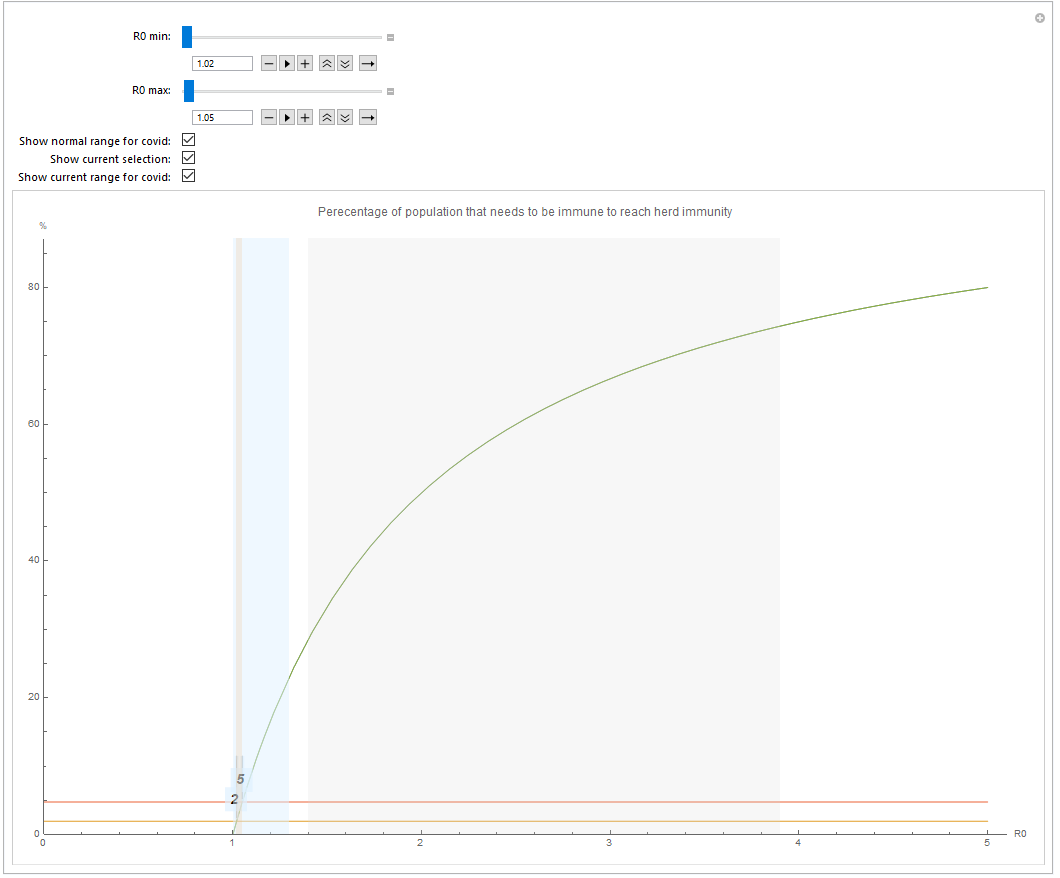
Of course these estimates are a bit rough, but they clearly give more hope that the measures taken in different countries are actually getting us towards herd immunity, if nothing else at least a policy dependent herd immunity. I plan to make a new post regarding how to use these policy dependent herd immunity to get towards a real herd immunity.

Attachments:

covid19-R0-and-h...nb