Wow, this is really amazing to see this in a gif format. Great job! Thanks for sharing this!

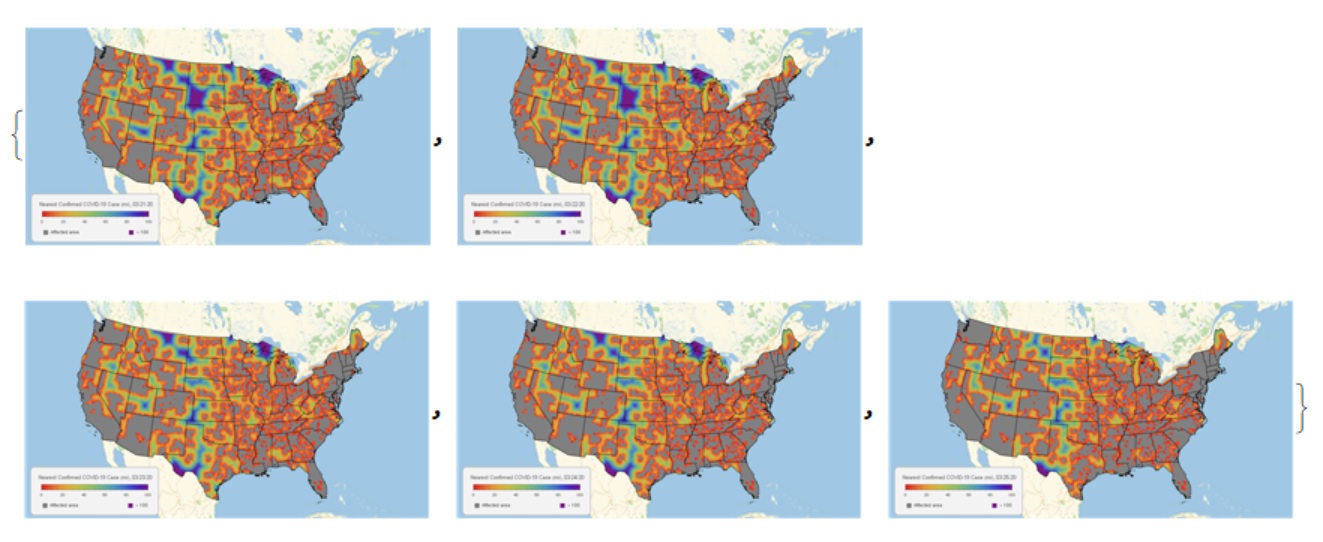
Thank you. Finally, I reproduced the result by changing the code as follows

COVID19CountyData = 
  ResourceFunction["NYTimesCOVID19Data"]["USCountiesTimeSeries"];

COVID19CountyData = 
  COVID19CountyData[All, "Cases", 
   TimeSeries[TimeSeriesInsert[#, {DateObject[{2020, 1, 20}], 0}], 
     ResamplingMethod -> {"Interpolation", 
       InterpolationOrder -> 0}] &];

COVID19CountyData = 
  COVID19CountyData[
   KeySelect[! MissingQ[#] && ! 
       MatchQ[#, Entity[_, {_, "Alaska" | "Hawaii", _}]] &]];

coord = CountryData["USA", "Polygon"][[1, 1, 1]];
bmr = BoundaryMeshRegion[coord, Line[Append[Range[Length[coord]], 1]]];

usatri = TriangulateMesh[bmr, MaxCellMeasure -> .1];

MeshRegion[
 TransformedRegion[usatri, 
  ReflectionTransform[{1, 0}]@*RotationTransform[\[Pi]/2]], 
 MeshCellStyle -> {0 -> {PointSize[Small], Red}, 1 -> {Thin, Black}}]
usagcomp = 
  GraphicsComplex[GeoPosition[MeshCoordinates[usatri]], 
   MeshCells[usatri, 2, "Multicells" -> True]];

usstates = 
  EntityClass["AdministrativeDivision", "ContinentalUSStates"];

usasamp = GeoPosition /@ MeshCoordinates[usatri];


countypolys = 
  EntityValue[Normal[Keys[COVID19CountyData]], "Polygon", 
   "EntityAssociation"];
COVID19DistanceMap[date_DateObject?DateObjectQ] := 
 Block[{counties, polys, coords, dists, gcomp, map, legend}, 
  counties = COVID19CountyData[Select[#[date] > 0 &]];
  polys = Lookup[countypolys, Normal[Keys[counties]]];
  coords = 
   GeoPosition /@ Join @@ Cases[polys, _List?MatrixQ, \[Infinity]];
  dists = 
   Clip[QuantityMagnitude[
     Nearest[coords -> "Distance", usasamp][[All, 1]], "Miles"], {0., 
     100.}];
  gcomp = 
   Append[usagcomp, 
    VertexColors -> ColorData[{"Rainbow", {-100, 0}}] /@ Minus[dists]];
  map = GeoGraphics[{GeoStyling[Opacity[1]], 
     gcomp, {Gray, polys}, {EdgeForm[Black], FaceForm[], 
      Polygon[usstates]}}, ImageSize -> 1024];
  legend = makeLegend[date];
  Legended[map, Placed[legend, {0.1725, 0.125}]]]

makeLegend[date_] := 
 Framed[Column[{BarLegend[{ColorData[{"Rainbow", 
          "Reversed"}][.01 #] &, {0, 100}}, LegendLayout -> "Row", 
     ImageSize -> 300, 
     LegendLabel -> 
      Style["\[ThinSpace]   Nearest Confirmed COVID\[Hyphen]19 Case \
(mi), " <> DateString[date, {"Month", "/", "Day", "/", "YearShort"}], 
       13, GrayLevel[0.2]]], 
    Row[{Spacer[24], 
      SwatchLegend[{Gray, ColorData["Rainbow", 0]}, {"Affected area", 
        "> 100"}, LegendMarkerSize -> 13, 
       LabelStyle -> GrayLevel[0.2], LegendLayout -> "Row", 
       Spacings -> {0.5, 10.5}]}]}, Spacings -> 0], 
  Background -> GrayLevel[0.95], RoundingRadius -> 10, 
  FrameStyle -> {AbsoluteThickness[1.5], GrayLevel[0.75]}, 
  FrameMargins -> {{0, 10}, {10, 15}}]

But the last piece of visualization code is very slow. How can this be accelerated?

frames = ParallelMap[Rasterize[COVID19DistanceMap[#]] &, 
  DateRange[DateObject[{2020, 3, 21}], DateObject[{2020, 3, 25}]], 
  Method -> "FinestGrained"]

In which version did you test this code? In version 12.1, this does not work. There is a message

$RecursionLimit::reclim2: Recursion depth of 1024 exceeded during evaluation of COVID19CountyData[All,Cases,TimeSeries[TimeSeriesInsert[#1,{DateObject[{2020,1,20}],0}],ResamplingMethod->{Interpolation,InterpolationOrder->0}]&].

Sorry, but it doesn’t work. Perhaps this is a bug of the type discussed on https://mathematica.stackexchange.com/questions/216746/user-interface-mathematica-12-1-terribly-slow

Thank you, this piece of code works now. But the second piece of code does not work in v.12.1,

usstates = 
  EntityClass["AdministrativeDivision", "ContinentalUSStates"];
usa = RegionUnion[
   BoundaryDiscretizeGraphics /@ usstates["Polygon"][[All, All, 1]]];
usatri = TriangulateMesh[usa, MaxCellMeasure -> .05];
usasamp = GeoPosition /@ MeshCoordinates[usatri];

We have messages

BoundaryMeshRegion::holm: Unable to find points not in the region for all of the inner boundaries.

BoundaryMeshRegion::holm: Unable to find points not in the region for all of the inner boundaries.

BoundaryMeshRegion::could not make representation: -- Message text not found -- (TriangleLinkMesh)

ToElementMesh::fememins: The mesh elements are not valid. A set of valid mesh element incidents needs to be positive integers and be able to form a complete sequence starting from 1 to the largest incident present. There are missing incidents; a complete sequence cannot be formed.

ToElementMesh::femtemnm: A mesh could not be generated.

I used the standard code to triangulate the mesh

coord = CountryData["USA", "Polygon"][[1, 1, 1]];
bmr = BoundaryMeshRegion[coord, Line[Append[Range[Length[coord]], 1]]];

usatri = TriangulateMesh[bmr, MaxCellMeasure -> .1];

MeshRegion[
 TransformedRegion[usatri, 
  ReflectionTransform[{1, 0}]@*RotationTransform[\[Pi]/2]], 
 MeshCellStyle -> {0 -> {PointSize[Small], Red}, 1 -> {Thin, Black}}]