First of all, it is possible to check the code that I am asking for because I know that $x=3051$ must yield at least a solution to the problem.
Well, I have the following system of equations:
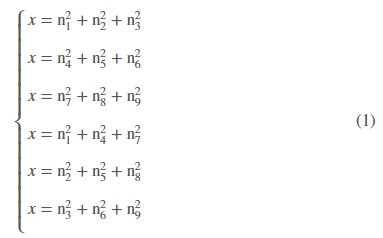
Now, I need to solve this system for {n1,n2,n3,n4,n5,n6,n7,n8,n9} . The values of $x$ that needs to be tried come from the following code:
ParallelTable[
If[TrueQ[Length[
Select[Select[PowersRepresentations[n, 3, 2], Times @@ # != 0 &],
Length[#] == Length[Union[#]] &]] >= 6], n, Nothing], {n, 0,
10000}]
(* {314,329,341,...,9998} *)
Question: How can I loop through the values given by the ParallelTable code ({314,329,341,...,9998}) in order to check if the system of equations gives a solution for a certain value of $x$?
So, the first case to check would be when $x=314$ and the solutions that has to be tried are given by:
Select[Select[PowersRepresentations[314, 3, 2], Times @@ # != 0 &],
Length[#] == Length[Union[#]] &]
(* {{1, 12, 13}, {3, 4, 17}, {3, 7, 16}, {5, 8, 15}, {7, 11, 12}, {8, 9,
13}} *)
So, we need to try to solve the following system of equations using the possible values, given from the code above ({{1,12,13},{3,4,17},{3,7,16},{5,8,15},{7,11,12},{8,9,13}}):
x=314;
Solve[{x == n1^2 + n2^2 + n3^2, x == n4^2 + n5^2 + n6^2,
x == n7^2 + n8^2 + n9^2, x == n1^2 + n4^2 + n7^2,
x == n2^2 + n5^2 + n8^2, x == n3^2 + n6^2 + n9^2}, {n1, n2, n3, n4,
n5, n6, n7, n8, n9}]