FiniteGroupData is missing a few group generations, so I've filled in some holes. One of the groups is Frobenius 21.
F21=PermutationGroup[{Cycles[{{1,2,3,4,5,6,7},{8,9,10,11,12,13,14},{15,16,17,18,19,20,21}}],Cycles[{{1,7,6,5,4,3,2},{8,14,13,12,11,10,9},{15,21,20,19,18,17,16}}],Cycles[{{1,8,15},{2,12,17},{3,9,19},{4,13,21},{5,10,16},{6,14,18},{7,11,20}}],Cycles[{{1,15,8},{2,17,12},{3,19,9},{4,21,13},{5,16,10},{6,18,14},{7,20,11}}]}];
Then I looked at the Cayley graph.
z =Graph3D[CayleyGraph[F21]]
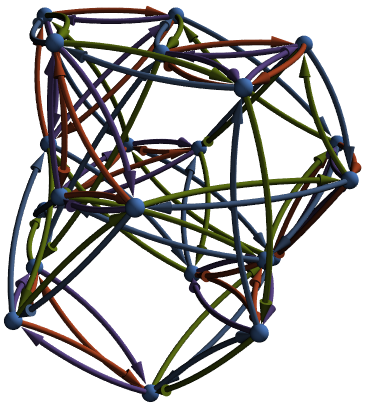
I decided to check if it was in GraphData. Turns out it is.
IsomorphicGraphQ[GraphData[{"UnitDistance",{21,2}}], Graph[UndirectedEdge@@@Union[Sort/@List@@@EdgeList[z]]]]
Which graph is this? Turns out this is my graph, a unit distance graph with chromatic number 4 and no 4-cycles.
GraphData[{"UnitDistance", {21, 2}}]
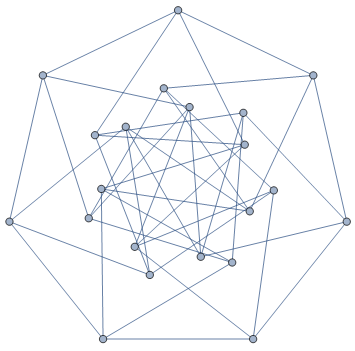
When I found the graph I had no idea it would pop up somewhere else.
In the notebook I also have some missing groups for orders 16, 18, 20, 21, 24 and 27. Does anyone want the missing groups for order 32?
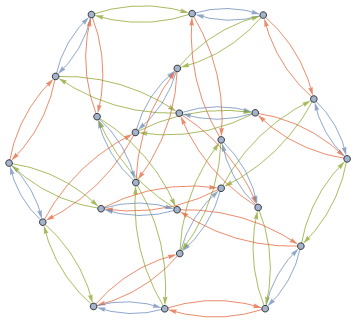
One of the 24 groups gives the Nauru graph.
 Attachments:
Attachments: