Vlado, here comes a slight extension:
First - as a side note - here is an improved siemensFunc:
siemensFunc[phases_Integer, px_, x_, y_] := Module[{r, \[Phi], rlim},
If[(x == 0) && (y == 0), Return[0]];
r = Norm[{x, y}];
\[Phi] = ArcTan[x, y];
rlim = px phases/Pi;
If[r > rlim, (Sin[phases \[Phi]] + 1)/2., (Sign[Sin[-2 \[Phi]]] + 1)/2.]
]
ll = 5.01;
px = 0.02; (* pixel size *)
siemensStarData = Table[siemensFunc[120, px, x, y], {y, -ll, ll + 1, px}, {x, -ll + 1, ll + 1, px}];
Image[siemensStarData]

But my remark here is basically about processing the test image you sent, and the main thing is a hopefully more robust function for finding the star centers:
findSiemensStarCenter[img_Image] :=
Module[{star, lines, linePairs, intersects},
star = SelectComponents[Binarize[img], #EnclosingComponentCount == 1 &];
lines = ImageLines[Binarize@star, MaxFeatures -> 15];
linePairs = Partition[lines, 2, 1];
intersects = (RegionIntersection /@ linePairs) /. EmptyRegion -> Nothing;
TrimmedMean[intersects[[All, 1, 1]], .2]
]
SetDirectory[NotebookDirectory[]];
(* assuming that your MMA notebook and the test image are in the same directory *)
testImg = Import["20191119_164554.bmp"];
(* extracting the 5 Siemens stars: *)
{dimx, dimy} = ImageDimensions[testImg];
parts = ImagePartition[testImg, {dimx/5, dimy/3}];
{topleft, topright, bottomleft, bottomright} = Extract[parts, {{1, 1}, {1, 5}, {3, 1}, {3, 5}}];
middle = ImageCrop[testImg, {700, 700}];
(* calculating its centers: *)
centers = findSiemensStarCenter /@ {topleft, topright, middle, bottomleft, bottomright}
You can concentrate all this using an Association:
siemensStars =
Association[
"TopLeft" -> Association["Image" -> topleft, "Center" -> centers[[1]]],
"TopRight" -> Association["Image" -> topright, "Center" -> centers[[2]]],
"Middle" -> Association["Image" -> middle, "Center" -> centers[[3]]],
"BottomLeft" -> Association["Image" -> bottomleft, "Center" -> centers[[4]]],
"BottomRight" -> Association["Image" -> bottomright, "Center" -> centers[[5]]]];
and than you can do things like siemensStars["BottomRight", "Center"] or siemensStars // Dataset. And you can convince yourself about the correctness of the above calculation like so:
cccircles[center_] := Table[Circle[center, r], {r, 15, 500, 30}]
Grid[KeyValueMap[{#1, HighlightImage[#2["Image"], cccircles[#2["Center"]]]} &, siemensStars], Frame -> All]
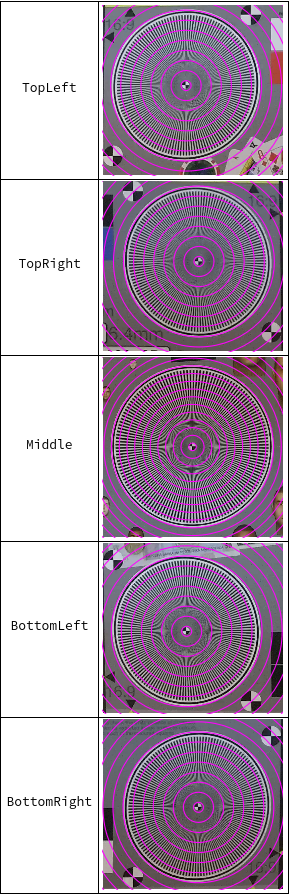
Maybe this serves as an inspiration.