Here comes a final remark - hopefully not too off-topic! I just want to mention the probably most basic and shortest way to determine the MTF:

The image of a "Delta peak" is the point spread function (PSF) - and its Fourier transform is the sought-after MTF. Making the realistic assumption of a rotational symmetric PSF, one can make use of the Fourier slice theorem: A projection of the 2D-PSF gives its Abel transform (1D), and the Fourier transform of the Abel transform gives the radial data of the (rotational symmetric) MTF:

(* image with a single white pixel ("Delta peak"): *)
data = ConstantArray[0, {500, 500}];
data[[250, 250]] = 1;
(* then blurred, i.e. "signal processing" *)
(imgPDF = Blur[Image[data], 3]) // ImageAdjust
dataPDF = ImageData[imgPDF];
(* adding all lines up = projection = Abel transform: *)
abel = Plus @@ dataPDF;
(* "signal processing" choice of FT: *)
mtf = Abs@Fourier[abel, FourierParameters -> {1, -1}];
ListLinePlot[mtf[[;; 250]], PlotRange -> All, PlotLabel -> "MTF", GridLines -> Automatic]

Hi Vlado, sorry for the delay! Here is a sketch of my approach for finally calculating the MTF (according to the formula you gave). I am assuming we have defined the above siemensStars association, then:

(* using the star in the center as example: *)
tc = siemensStars["Middle", "Center"];
timg = ImageAdjust@ColorConvert[siemensStars["Middle", "Image"], "Grayscale"];
(* dummy image with identical dimensions for getting pixel positions: *)
tdim = ImageDimensions[timg];
(* circle with a radius of e.g. 200 pixels: *)
dummyImg = Thinning@Binarize@ColorNegate@Image[Graphics[Circle[tc, 200],            PlotRange -> Transpose[{{0, 0}, tdim}]], ImageSize -> tdim];
pixpos = DeleteDuplicates@PixelValuePositions[dummyImg, .8, .2];
(* angles of pixel positions: *)
angles = ArcTan[#1 - First[tc], #2 - Last[tc]] & @@@ pixpos;
(* pairs {angle, pixelValue} sorted by angle: *)
tvals = SortBy[Transpose[{angles, PixelValue[timg, pixpos]}], First];
timg + dummyImg

(* making a TimeSeries out of it for simplicity: *)
tvs = TimeSeries[tvals];
(* calculation of Min and Max: *)
ListLinePlot[{tvs, maxf = MaxFilter[tvs, 0.1], minf = MinFilter[tvs, 0.1]}]

(* calculation of MTF: *)
w = Mean[maxf];
b = Mean[minf];
mtf = (w - b)/(w + b)

I hope this helps! But I am afraid I will not have the time of digging any deeper into this project.

Best regards -- Henrik

Vlado, here comes a slight extension:

First - as a side note - here is an improved siemensFunc:

siemensFunc[phases_Integer, px_, x_, y_] := Module[{r, \[Phi], rlim},
  If[(x == 0) && (y == 0), Return[0]];
  r = Norm[{x, y}];
  \[Phi] = ArcTan[x, y];
  rlim = px phases/Pi;
  If[r > rlim, (Sin[phases \[Phi]] + 1)/2., (Sign[Sin[-2 \[Phi]]] + 1)/2.]
  ]

ll = 5.01;
px = 0.02; (* pixel size *)
siemensStarData = Table[siemensFunc[120, px, x, y], {y, -ll, ll + 1, px}, {x, -ll + 1, ll + 1, px}];
Image[siemensStarData]

But my remark here is basically about processing the test image you sent, and the main thing is a hopefully more robust function for finding the star centers:

findSiemensStarCenter[img_Image] := 
 Module[{star, lines, linePairs, intersects},
  star = SelectComponents[Binarize[img], #EnclosingComponentCount == 1 &];
  lines = ImageLines[Binarize@star, MaxFeatures -> 15];
  linePairs = Partition[lines, 2, 1];
  intersects = (RegionIntersection /@ linePairs) /. EmptyRegion -> Nothing;
  TrimmedMean[intersects[[All, 1, 1]], .2]
  ]

SetDirectory[NotebookDirectory[]];
(* assuming that your MMA notebook and the test image are in the same directory *)
testImg = Import["20191119_164554.bmp"];

(* extracting the 5 Siemens stars: *)
{dimx, dimy} = ImageDimensions[testImg];
parts = ImagePartition[testImg, {dimx/5, dimy/3}];
{topleft, topright, bottomleft, bottomright} = Extract[parts, {{1, 1}, {1, 5}, {3, 1}, {3, 5}}];
middle = ImageCrop[testImg, {700, 700}];

(* calculating its centers: *)
centers = findSiemensStarCenter /@ {topleft, topright, middle, bottomleft, bottomright}

You can concentrate all this using an Association:

siemensStars = 
  Association[
   "TopLeft" -> Association["Image" -> topleft, "Center" -> centers[[1]]], 
   "TopRight" -> Association["Image" -> topright, "Center" -> centers[[2]]],
   "Middle" -> Association["Image" -> middle, "Center" -> centers[[3]]], 
   "BottomLeft" -> Association["Image" -> bottomleft, "Center" -> centers[[4]]], 
   "BottomRight" -> Association["Image" -> bottomright, "Center" -> centers[[5]]]];

and than you can do things like siemensStars["BottomRight", "Center"] or siemensStars // Dataset. And you can convince yourself about the correctness of the above calculation like so:

cccircles[center_] := Table[Circle[center, r], {r, 15, 500, 30}]
Grid[KeyValueMap[{#1, HighlightImage[#2["Image"], cccircles[#2["Center"]]]} &, siemensStars], Frame -> All]

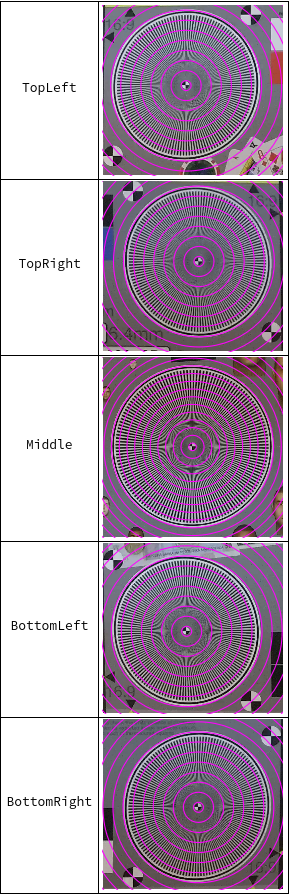
Maybe this serves as an inspiration.

Thank you Hans, thank You Henrik, The last response from Henrik seems to be what I am after, and it is very promising. I am not sure why you didn't see the original image I had attached in my last response, as I used the "Add file to the post". But I am now attaching the original real export of a CCTV camera (typically they are HD or 4k resolution) and the measurements that I have made using Matlab. As you can see I am also measuring other parameters of the reproduced test chart, like the colour, Gamma and noise. I am not very happy with the Siemens star measurements, as they are not consistent with what I measure manually using PhotoShop for example. This is the reason I intend to try Mathematica, which I have no experience with, but willing it to try. I am assuming, finding the colour coordinates of the colour patches would be easy, and so would the random pixel noise of a grey patch representing 50% grey. Thank you very much for this hint Henrik, I will try and reproduce it myself on the real test chart and calculate the Depth of Modulation.

Attachments:

20191119_164554.bmp

Evaluation-cam-1.jpg

Noise at 50percent.jpg

SFR maximum for ...png

Vlado, this seems to be an interesting topic, but without any typical test image it is hard to say anything.

A test chart has 5 Siemens stars, one larger one in the centre and four smaller in each corner. [...] I have attached a real camera export ...

So, where is it?

Ok Hans, this is what i would summarise it as: 1. A test chart has 5 Siemens stars, one larger one in the centre and four smaller in each corner. An image is taken by a camera and exported as JPG or BMP. How would you find the five circles and their centres? 2. Once the circles are found and their respective centres, one needs to measure the Depth of Modulation, as per the image I attached previously. Basically find how close to the centre the B/W rays are distinguishable with 10% contrast. 3. Based on the measurement under 2 (In pixels) calculate the MTF expressed in Line Pairs per Picture height. This is admittedly very easy if 1 and 2 are automated. I have attached a real camera export, which means they could always be slight variations in star positions, their geometry could be distorted (not always perfect circles) and have different resolution (which is to be measured).