I'm using Mathematica to create this graphic and would like to be able to add points around a few more of the concentric circles without writing 2^n lines of code for each one. As you can see below, I created this by setting each Graphics and Graphics to a variable (like a4 or g3) then by calling Show on each. Is there a way to use While or For to do this, or some other solution where the points can be created with fewer lines of code. Thank you!
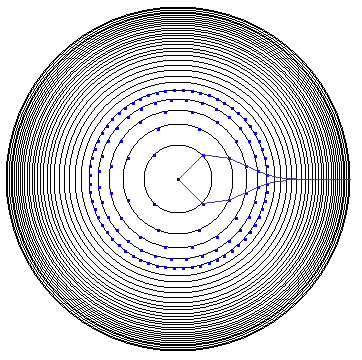
How do I make the next circle have points at (Log[2,7] Cos Pi/128, Log[2,7] Sin Pi/128),
then (Log[2,7] Cos 3 Pi/128, Log[2,7] Sin 3 Pi/128), etc.,
all the way to (Log[2,7] Cos 255 Pi/128, Log[2,7] Sin 255 Pi/128)?
I've included portions of my code below.
g0 = Graphics[Circle[{0, 0}, Log[2, 2]]]
g1 = Graphics[Circle[{0, 0}, Log[2, 3]]]
g2 = Graphics[Circle[{0, 0}, Log[2, 4]]]
...
a8 = Graphics[ Point[{Log[2, 3] Cos[Pi/8], Log[2, 3] Sin[Pi/8]}, VertexColors -> {Blue}]]
a9 = Graphics[ Point[{Log[2, 3] Cos[3 Pi/8], Log[2, 3] Sin[3 Pi/8]}, VertexColors -> {Blue}]]
a10 = Graphics[ Point[{Log[2, 3] Cos[5 Pi/8], Log[2, 3] Sin[5 Pi/8]}, VertexColors -> {Blue}]]
a11 = Graphics[ Point[{Log[2, 3] Cos[7 Pi/8], Log[2, 3] Sin[7 Pi/8]}, VertexColors -> {Blue}]]
...
a127 = Graphics[ Point[{Log[2, 6] Cos[127 Pi/64], Log[2, 6] Sin[(127 Pi/64]}, VertexColors -> {Blue}]]
Show[g0, g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, \g15, g16, g17, g18, g19, g20, g21, g22, g23, g24, g25, g26, g27, g28, \g29,...]