Jim Williams recently finished a multi-year search for all simple perfect squared squares up to order 37. More details will eventually be at squaring.net. For orders 21 to 37, there are {1, 8, 12, 26, 160, 441, 1152, 3001, 7901, 20566, 54541, 144161, 378197, 990981, 2578081, 6674067, 17086918} such squares (A006983).
Bouwkamp codes for the smallest squares of each order (A129947 A217148) are as follows.
smallest={{21,112,112,50,35,27,8,19,15,17,11,6,24,29,25,9,2,7,18,16,42,4,37,33},{22,110,110,60,50,23,27,24,22,14,7,16,8,6,12,15,13,2,28,26,4,21,3,18,17},{23,110,110,44,29,37,21,8,13,32,28,16,15,19,12,4,3,1,2,14,5,10,41,38,7,31},{24,120,120,47,32,41,15,17,8,33,19,20,23,25,14,5,4,13,3,10,16,9,12,46,40,6,34},{25,147,147,74,73,32,41,40,34,15,17,6,16,12,14,9,13,10,8,33,27,25,5,4,3,23,20,19},{26,212,212,99,57,56,1,55,26,32,20,6,38,48,19,28,4,24,16,39,12,7,5,2,85,23,17,65,62},{27,180,180,89,48,43,12,31,41,7,19,50,40,25,36,29,15,10,23,6,9,1,56,21,16,51,4,13,39,34},{28,201,201,77,56,68,21,17,18,6,30,32,4,13,24,54,38,10,1,12,11,39,36,2,34,16,22,70,3,67,64},{29,221,221,100,68,53,15,38,32,28,23,5,56,33,62,41,29,44,18,21,20,74,1,7,12,59,19,6,13,8,48,40},{30,201,201,77,55,69,41,14,27,56,51,26,8,15,45,25,1,9,2,13,11,7,17,16,40,73,3,10,60,28,4,36,32},{31,215,215,92,68,55,13,42,24,26,31,50,28,15,23,21,5,2,40,38,7,8,6,1,17,36,22,12,10,19,78,73,9,64},{32,185,185,80,51,54,29,19,3,16,41,10,25,35,26,43,15,28,20,33,9,17,36,8,7,13,1,6,30,62,5,57,34,2,32},{33,223,223,98,69,56,12,20,24,1,3,8,42,26,2,5,19,10,4,6,22,16,45,57,28,13,38,15,40,18,25,83,11,7,72,68},{34,218,218,79,61,78,18,43,36,42,41,31,25,11,47,10,9,17,5,40,6,16,1,8,35,7,48,28,4,20,67,26,14,63,12,50,38},{35,225,225,95,70,60,22,38,28,30,12,18,16,58,34,3,31,2,52,50,24,20,21,14,5,1,4,13,32,75,72,10,9,27,19,8,43,35},{36,253,253,96,81,76,36,40,18,63,69,24,3,21,32,4,44,45,47,28,20,15,29,8,12,88,26,19,17,1,14,13,9,64,62,23,7,16,39},{37,237,237,93,79,65,14,51,56,37,49,44,19,69,32,43,18,26,36,13,23,8,34,21,11,59,30,24,17,52,9,12,40,3,15,6,35,7,29,22}};
Using the code from the previous link.
Grid[Partition[ShowQuilt[#, True, 200] & /@ smallest, UpTo[6]]]
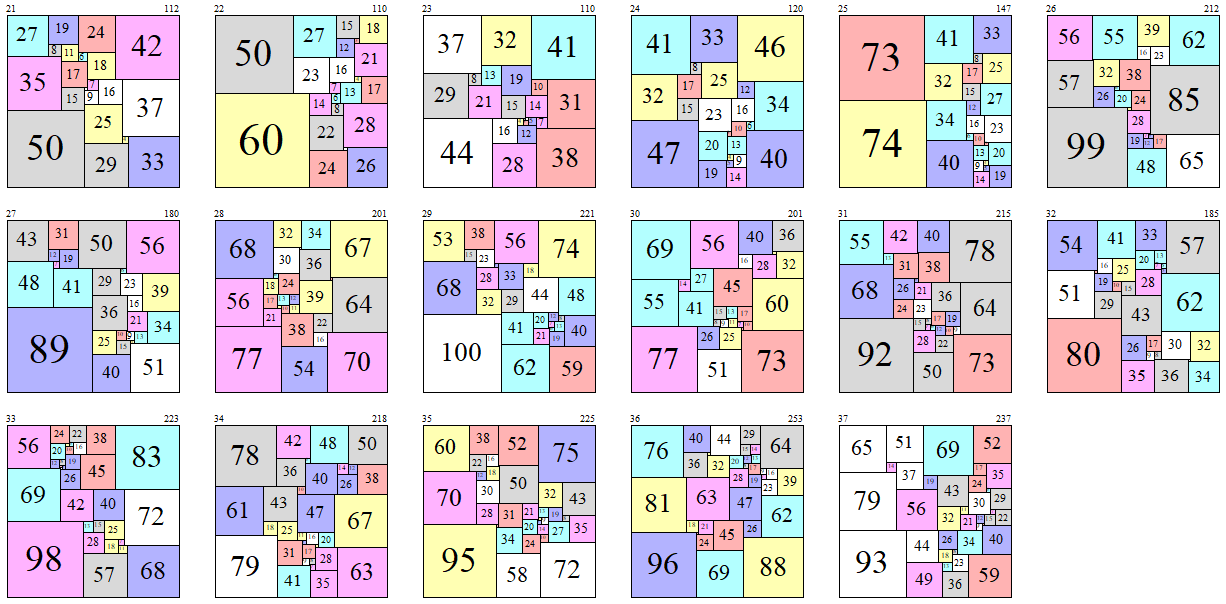
The largest squares (A217149) are as follows:
largest = {{21,112,112,50,35,27,8,19,15,17,11,6,24,29,25,9,2,7,18,16,42,4,37,33},{22,192,192,86,49,57,41,8,28,37,19,9,47,35,4,31,14,10,36,17,26,12,71,62,59},{23,332,332,123,89,120,58,31,83,68,49,50,24,26,56,48,1,47,30,15,53,17,129,38,112,91},{24,479,479,175,140,164,35,29,52,24,28,160,6,23,130,86,43,60,26,17,77,44,68,174,5,155,150},{25,661,661,262,196,203,83,106,7,210,161,84,17,36,41,23,18,111,31,5,64,77,38,102,73,248,238,175},{26,825,825,302,277,246,57,189,25,117,109,26,235,92,83,8,135,49,90,127,81,157,53,37,5,76,304,288,233},{27,1179,1179,484,316,379,108,145,63,82,360,42,66,29,198,18,24,308,194,119,69,50,168,80,114,149,440,387,35,352},{28,1544,1544,649,439,456,214,208,17,473,6,55,147,385,260,4,175,49,104,12,135,116,81,94,125,216,203,7,615,510,419},{29,2134,2134,855,562,717,338,224,69,648,293,518,292,45,204,179,186,286,43,161,226,109,100,9,91,265,17,174,165,769,761,604},{30,2710,2710,992,782,936,210,418,154,264,826,737,465,242,440,15,227,272,208,29,289,122,64,140,4,260,981,92,948,16,124,108,781},{31,3641,3641,1460,991,1190,402,390,199,337,1052,12,247,131,67,347,927,600,116,15,352,112,251,320,139,379,363,327,593,16,1399,395,1254,988},{32,4988,4988,1833,1462,1693,436,428,367,231,442,1482,61,306,1399,369,65,205,284,304,197,402,39,709,323,673,378,347,725,331,357,694,1813,1756,1419},{33,6391,6391,2494,1899,1998,704,1096,99,2097,1615,770,109,421,392,210,377,901,240,181,224,167,845,165,544,389,291,98,20,682,199,662,2296,2282,469,1813},{34,8430,8430,3184,2486,2760,687,747,778,274,504,2530,11,492,184,2074,1121,124,592,31,1313,308,640,160,752,953,808,536,816,713,145,1199,3172,103,3140,919,2118},{35,11216,11216,4067,3287,3862,780,1404,1103,528,3334,3183,1664,301,1330,634,496,575,138,279,79,200,454,406,366,225,254,591,562,1476,1519,551,1704,790,4020,3966,736,3230},{36,15039,15039,5596,5143,4300,1315,2985,453,2629,1589,472,3873,2176,726,1061,391,335,787,609,1249,731,941,2653,755,763,1697,2899,209,1221,237,984,8,1712,1469,736,5570,5101,4368},{37,20242,20242,8073,5209,6960,3458,1751,2543,6168,4729,2750,594,1680,1536,836,700,2679,896,1340,476,1204,1979,1247,452,444,1145,639,519,1137,732,1034,2372,946,416,1866,7440,1450,7114,5688}}
With corresponding images: 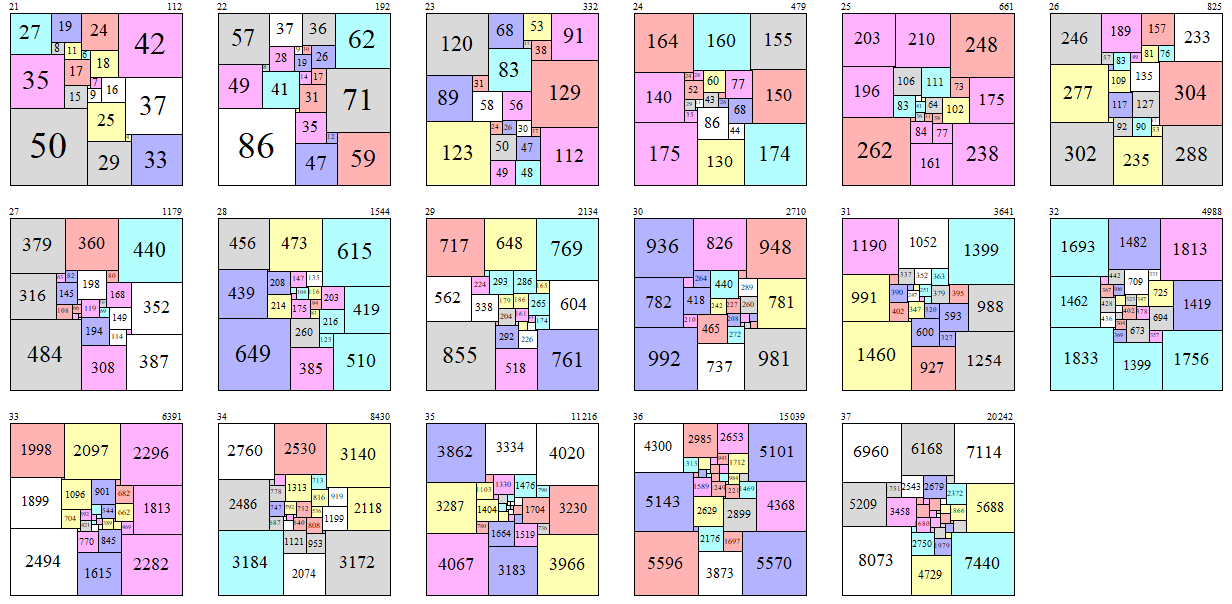
Order 38 is expected to be too large to analyze for at least a few years. Then again, Order 37 was considered impossible a decade ago.