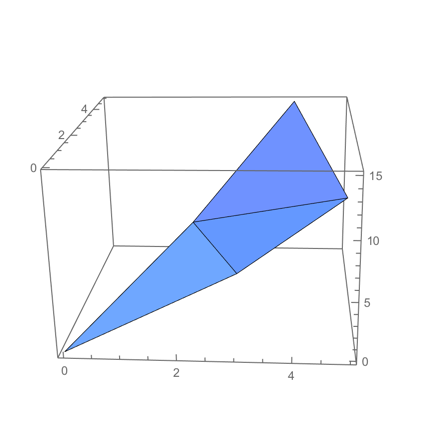
I am unsure if this is what you are looking for, but perhaps it will help:
data3D = {{2, 3, 6},
{3, 1, 5},
{4, 5, 15},
{5, 2, 10},
{0, 0, 0}
}
Needs["TetGenLink`"]
Use a convex hull:
{pts, surface} = TetGenConvexHull[data3D];
Graphics3D[GraphicsComplex[pts, Polygon[surface]]]
Write a function that determines the normal of a triangle, which can be applied to pts and surface
normal[xyz_, vertList_] := Block[
{u, v},
u = xyz[[vertList[[2]]]] - xyz[[vertList[[1]]]];
v = xyz[[vertList[[3]]]] - xyz[[vertList[[2]]]];
Cross[u, v]
]
Select only those triangles which have their normals pointing up:
bottomTriangles = Select[surface, (normal[pts, #].{0, 0, 1} > 0) &]
Graphics3D[GraphicsComplex[pts, Polygon[bottomTriangles]],
Axes -> True, BoxRatios -> {1, 1, 2/3}]