Hi,
I would like find a way to figure out how many unique collision there are between 2 equally subdivided ellipsoids (velocity=1).
When you have 2 ellipsoids and you let them collide than you have an infinite amount of possible collisions.
The goal is to reduce this infinite number to a manageable list of for example unique 32 collisions by :
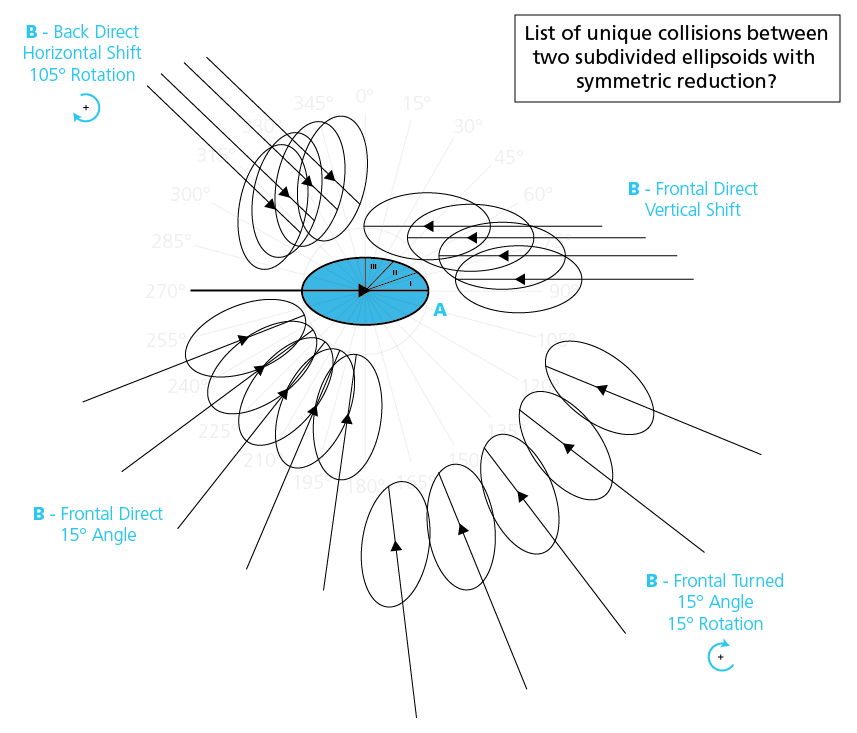
- Subdividing the ellipsoids, so instead of having an infinite number of points on these ellipsoids where they can hit, they are subdivided into 3 zones (I-II-III per quarter).
- Reduce the possible rotation angles into steps of 15°
- Using symmetry, to cancel out the collisions that are the same when A hits B vs. B hits A, and the outcome of a collision on the left side is symmetric to one on the right, or back and front etc.
(Note, the use of 3 Zones and 15° Angles is arbitrary, i guess once a method is found these could be easily changed into whatever.)
--
Attached is an overview where the Ellipse
A is Set and
B comes flying in, and where:
- B is shifted a couple of steps along the vertical-axis (right-top).
- B is rotated in relation to A in steps of 15° (left-bottom)
- B is rotated in relation to A in steps of 15° and B itself is rotated 15° (right-bottom)
- B is shifted a couple of steps along the horizontal-axis and B itself is rotated 105°(left-top).
-
That's it, I don't know if such a method already exists or if this is perhaps something that could be solved with a Monte Carlo method or something else, all suggestions are welcome to take care of this.
Kind regards,
m.