Hi all!
I'm new around here, so I apologise if my post is in the wrong place, or is irrelevant, or perhaps ignorant. I have been having a blast playing around with Wolfram Models, and today I stumbled upon an interesting set of evolutions: 
I wonder if anybody else has found any results like this previously. I was hoping somebody with a bit more experience could do some extra analysis on this as it does appear to exhibit some strange behaviour, for example, the entire hypergraph flips on the 8th evolution:
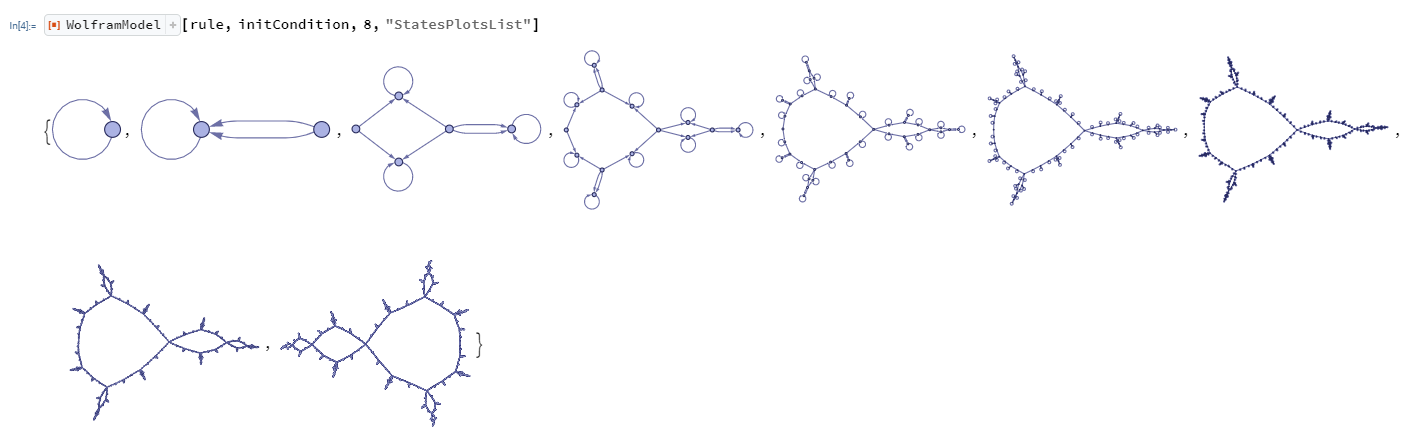
This seems very very strange to me, as I had previously believed that the mandelbrot set could only be generated in the complex plane? This seems to suggest that a simple arbitrary rule involving simple relationships can generate something previously only found in the complex plane. Please let me know if I am way off in this, as I do not pretend to be a high-level mathematician, I am in the infancy stages of this pursuit.
Some interesting discussion and other similar hypergraphs are welcomed! I really would love to see more iterations of this rule however I currently only have access to the Cloud version of the Wolfram environment, so I am limited to 9 evolutions. Looking forward to a cool chat!