Message Boards Message Boards

Mandelbrot Set found as a rule for WolframModel Hypergraphs

Jacob Brooke
Posted 4 years ago

Hi all!

I'm new around here, so I apologise if my post is in the wrong place, or is irrelevant, or perhaps ignorant. I have been having a blast playing around with Wolfram Models, and today I stumbled upon an interesting set of evolutions: Mandelbrot Set Emergence

I wonder if anybody else has found any results like this previously. I was hoping somebody with a bit more experience could do some extra analysis on this as it does appear to exhibit some strange behaviour, for example, the entire hypergraph flips on the 8th evolution:

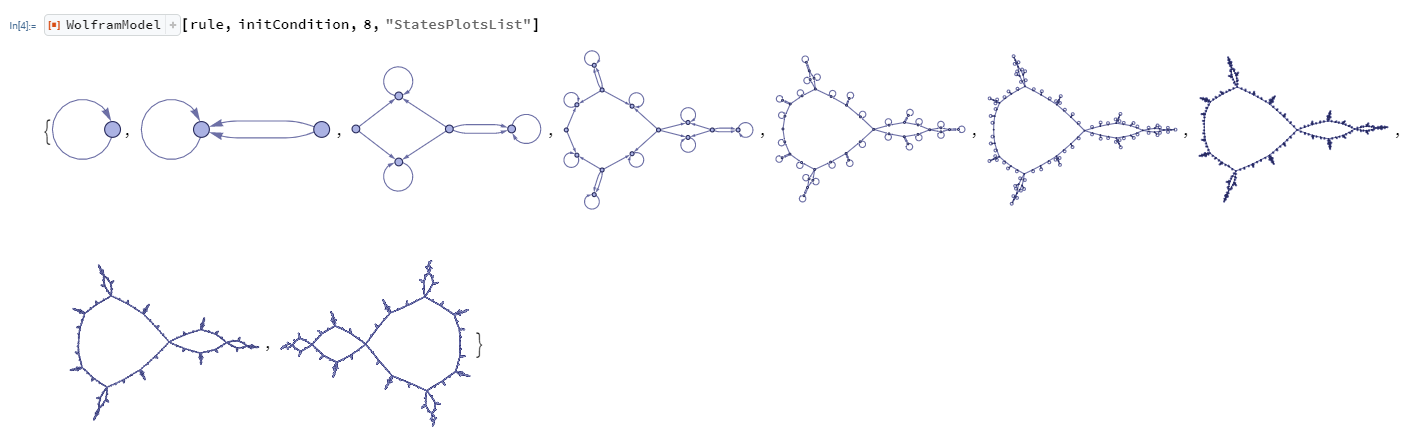
8th Evolution Flip

This seems very very strange to me, as I had previously believed that the mandelbrot set could only be generated in the complex plane? This seems to suggest that a simple arbitrary rule involving simple relationships can generate something previously only found in the complex plane. Please let me know if I am way off in this, as I do not pretend to be a high-level mathematician, I am in the infancy stages of this pursuit.

Some interesting discussion and other similar hypergraphs are welcomed! I really would love to see more iterations of this rule however I currently only have access to the Cloud version of the Wolfram environment, so I am limited to 9 evolutions. Looking forward to a cool chat!
POSTED BY: Jacob Brooke
5 Replies
Sort By:

This rule was actually illustrated in Stephen Wolfram's article, "A Class of Models with the Potential to Represent Fundamental Physics" at the beginning of Section 3.5: "Rules Depending on a Single Binary Relation". Stephen however, expressed it as: "{{x,y}}->{{z,z},{x,z},{y,z}}", and surprisingly, did not mention Mandelbrot. I only mention it now because at the time, I too saw the correspondence..
POSTED BY: David Stephenson

Wow! Didn't even know that was possible..! Impresssive.
POSTED BY: Pedro Cabral

Hi Jacob,

In Stephen's technical introduction paper (https://www.wolframphysics.org/technical-introduction/typical-behaviors/rules-depending-on-a-single-binary-relation/) he specifically mentions this behavior:

Several distinct classes of behavior are visible. Beyond simple lines, loops, trees and radial “bursts”, there are nested (“cactus-like”) graphs such as enter image description here obtained from the rule {{x, y}} → {{z, z}, {x, z}, {y, z}} enter image description here

I ran the rule to 10 steps and it does appear to flip after step 8 back and forth.

Anton
POSTED BY: Anton Spektorov
Jacob Brooke
Jacob Brooke
Posted 4 years ago

Hey Anton,

Thanks for the informative comment! I'll be sure to read more of the technical document as I had a hunch that this kind of pattern would very easily and naturally emerge from a repeated set replacement algorithm. But I was still surprised when I initially saw the similarities!

Warm regards, Jacob
POSTED BY: Jacob Brooke
Mike Besso
Mike Besso
Posted 4 years ago

Jacob:

I binged some YouTubes on Mandelbrot sets and Mandelbrot-like sets when I was "guaranteed" a few months ago.

If you search for Mandelbrot videos, you will find a few more examples like the one you found.
POSTED BY: Mike Besso
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract