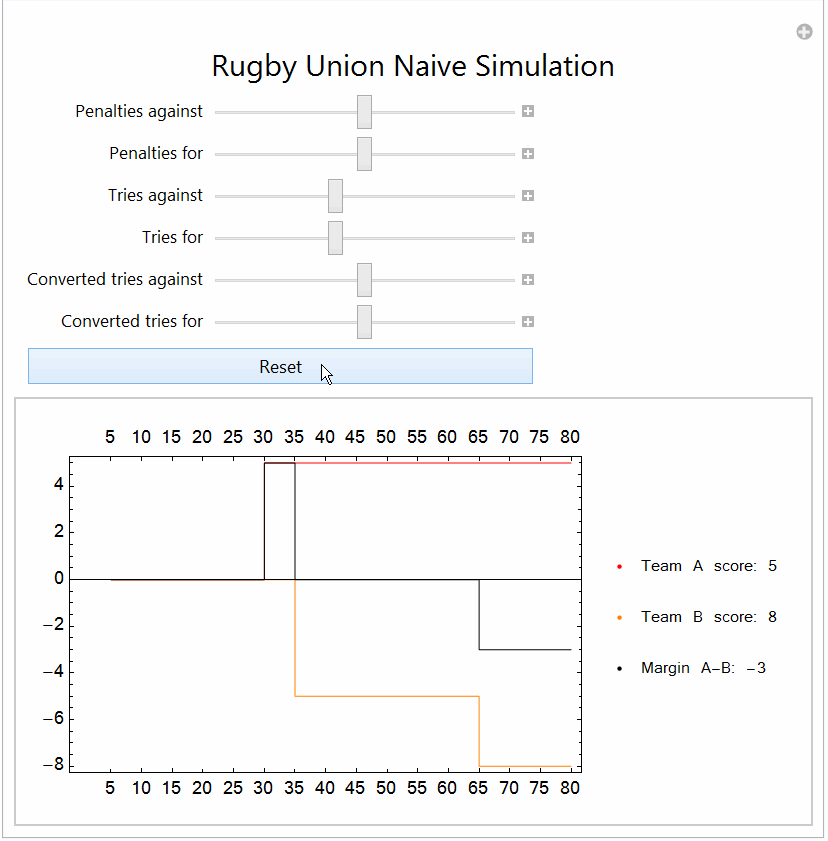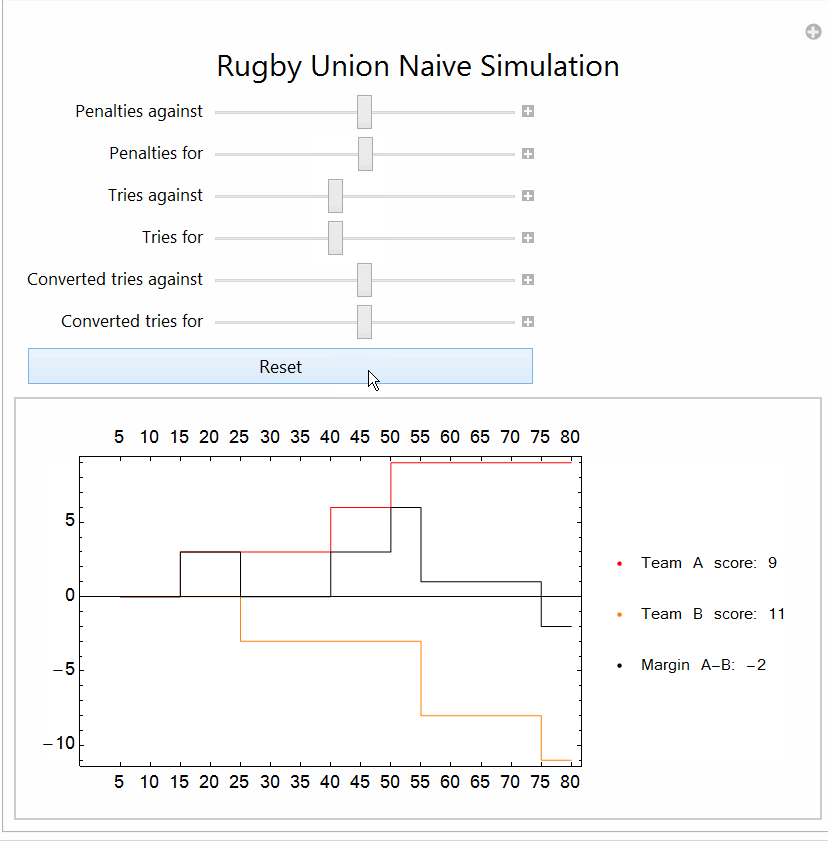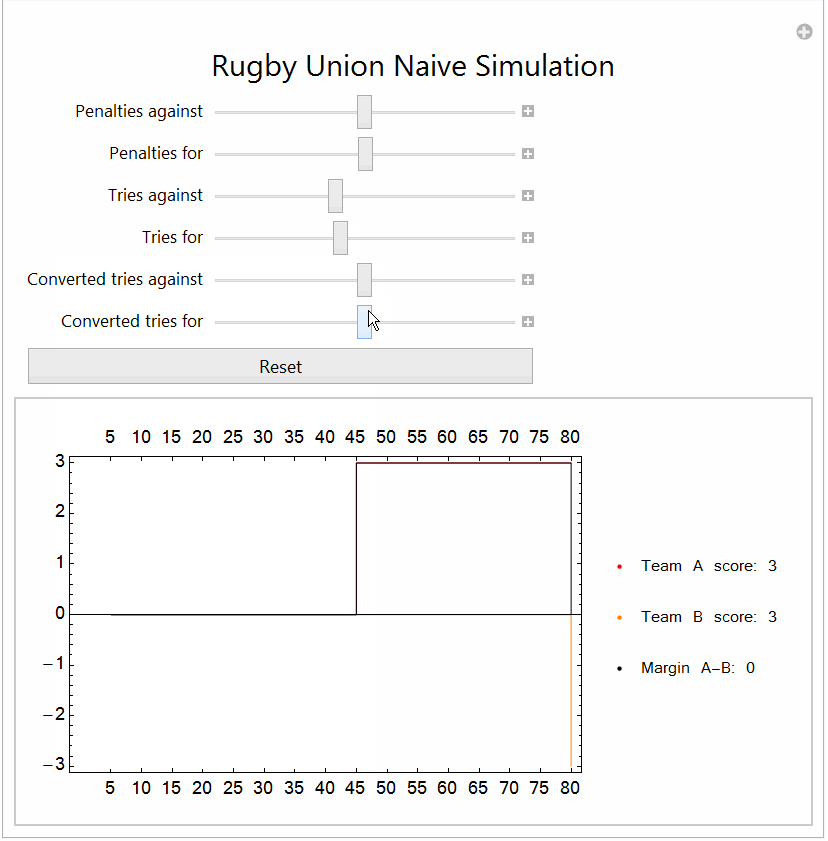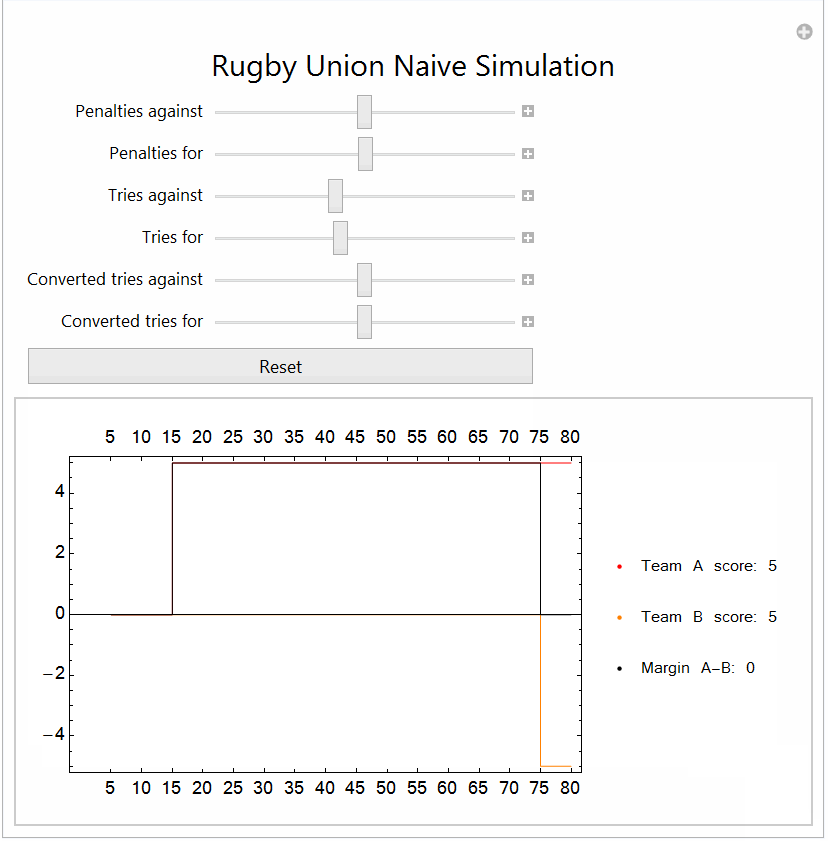
I post this not as an answer, viz, speeding up code but as potential motivating alternate approaches. I am not sure what the ultimate aim is: simulation, modelling, prediction.
My point is to illustrate some of the Mathematica's functionality for simulation.
In the following toy example there are a number of naive assumptions:
- essentially it is a simulation of a random walk with fixed probabilities of events: nothing, penalty for/against, try for/against, converted try for/against.
- the time intervals were discrete and regular 5 minute intervals (trying to be a little closer to reality, as two converted tries in a minute...hmm not going to happen)
- there is no dependency or autocorrelation structure: so does not deal with run of penalties increasing probability of try; "momentum" etc
I present it for 'fun' not realism with all its limitations.
Manipulate[
ed = EmpiricalDistribution[
Rescale[{100, pa, pf, ta, tf, cta, ctf}] -> {0, -3, 3, -5, 5, 7,
7}];
rv = RandomVariate[ed, 16];
margin = Accumulate@rv;
teama = Accumulate@(rv /. x_?Negative -> 0);
teamb = Accumulate@(rv /. x_?Positive -> 0);
legend =
Style[#, FontFamily -> "Kartika", 10] & /@ {StringForm[
"Team A score: ``", Last@teama],
StringForm["Team B score: ``", -Last@teamb],
StringForm["Margin A-B: ``", Last@margin]};
ListPlot[{teama, teamb, margin}, Joined -> True,
PlotStyle -> {Red, Orange, Black}, InterpolationOrder -> 0,
PlotLegends -> legend, BaseStyle -> {FontFamily -> "Kartika", 12},
Frame -> True,
FrameTicks -> {Thread[{Range[16], 5 Range[16]}], Automatic}]
,
{{pa, 25, "Penalties against"}, 20, 30}, {{pf, 25, "Penalties for"},
20, 30}, {{ta, 7, "Tries against"}, 5, 10}, {{tf, 7, "Tries for"},
5, 10}, {{cta, 3, "Converted tries against"}, 1,
5}, {{ctf, 3, "Converted tries for"}, 1, 5},
Button["Reset", rv = RandomVariate[ed, 16]],
BaseStyle -> {FontFamily -> "Kartika", 20},
FrameLabel -> {None, None, Style["Rugby Union Naive Simulation", 20],
None}]