This system of equations contains two nonlinear equations, and therefore cannot be solved in closed form.
They can be solved numerically with ParametricNDSolve that will allow you to play with the parameters.
{ss, ii, rr} = {s, i, r} /.
ParametricNDSolve[{eqns, {s[0] == s0, i[0] == i0, r[0] == r0}}, {s,
i, r}, {t, 0, 100}, {s0, i0, r0, \[Beta], g, m}]
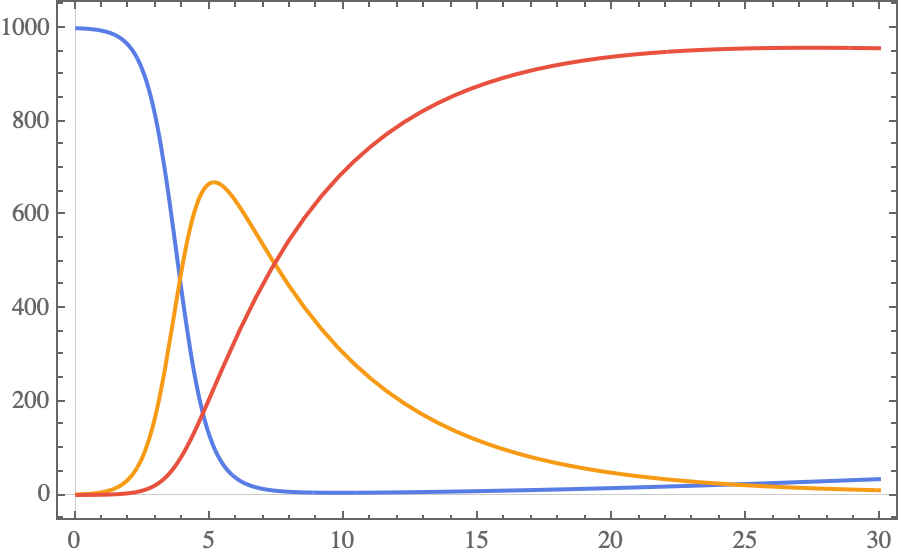
The following Plot can be put inside of Manipulate
Plot[{ss[1000, 1, 0, 0.002, 0.2, 0.003][t],
ii[1000, 1, 0, 0.002, 0.2, 0.003][t],
rr[1000, 1, 0, 0.002, 0.2, 0.003][t]}, {t, 0, 30}]