Introduction
The goal of this post is to start from images like this example one :

and generate pictures like:

or

Mathematica at least 12.1 will be required since Mixed Integer programming is used.
Explanation
Let's take the first image (black and white) as an example.
Let's assume we have a collection of 16 tiles:

The problem to solve is how to place the tiles on the picture so that the gray content of a tile is close to the gray content of the picture below it and at the same time the topological constraints are satisfied.
By topological constraints, I mean that the tiles must be compatible.
This is allowed:

This is forbidden because the dark horizontal band is continuing as a white horizontal band.

We are going to translate this problem into a set of equations on integer variables and with a linear cost function to optimize. The final problem will be solved with the LinearOptimization function from Mathematica 12.1.
Each pixel of the image is encoded by a vector 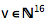 because there are 16 different tiles in this example. The components of the vector can be either 0 or 1.
because there are 16 different tiles in this example. The components of the vector can be either 0 or 1.
This is expressed as:
VectorLessEqual[{0, v}], VectorLessEqual[{v, 1}], v \[Element] Vectors[nbTiles, Integers]
For each pixel, only one tile can be used. We cannot put several tiles on a pixel but only choose one and only one.
If we use the constraint:
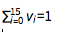
then we express that only one tile can be used. Indeed, since the component are integers and equal to 0 or 1, then the only way to satisfy this equation is that one of the components, and only one, is equal to one.
Expressing the topological constraints is similar.
We have equations like:
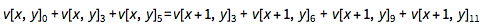
This equation is describing a relationship between pixel (x,y) and pixel (x+1,y).
The values on left and right side can either be 0 or 1 (at same time). When zero it means : none of the tiles is used. When one, it means one of the tile is used. So, the translation of the equation is:
If the tile 0,3 or 5 are used at pixel (x,y) then the tiles 3,6,9 or 11 must be used at pixel (x+1,y).
(I have not checked if it makes sense with the set of tiles I am using as example. The constraints for those tiles are probably different.).
To describe the topological constraint of the tiles, we have functions like:
rightSide[tileA[{a_,b_,c_}]] :={b,c};
This is giving a key describing the right side of the tile. Those keys are then used in associations to build the topological constraints. The key can be anything so if you want to add new tiles, you can just use the key you want to describe the sides of your tiles.
The generic function rightSide must be extended with new cases when new tiles are added.
Then, we need to express how good the tiles are approximating the original picture.
For this, an error function is created. It is a sum of terms:

It means that if the tile i is selected for pixel (x,y) then the approximation error is Subscript[f, k]
The function averageColor must be extended with new tiles. It returns the color content of a tile : a RGBColor. The code is using a color distance to compute the errors.
That's why the input picture is always converted to RGB and the alpha channel removed.
So, finally we have translated our problem into a set of integer constraints and with a linear cost function to optimize. It is a mixed integer programming problem which can be solved with LinearOptimization.
The tiles must be displayed. It is done by the function tileDraw and the tile is drawn in a square from (0,0) to (1,1) corners. The code is rasterizing those graphics into 50x50 pixel images.
I have had lots of problems with those pictures due to rounding errors ... probably due to the very old GPU on my very old computer. So I tuned the vector code assuming the final tile image is 50x50 pixels. Now the pictures are well aligned, there is no more one row or one column of wrong pixels on the boundary of the tiles.
But this may cause a problem on your configuration. So, if the tile pictures are not rendering correctly on your side, you'll need to tune my vector graphic code again.
If the picture is too big, solving the full mixed integer programming problem may take too long. But we can solve a sub-optimal problem. We divide the picture into sub-pictures and solve the problem on each sub-picture then we recombine the solutions. For it to work : we must add new constraints to express compatibility between the pictures.
For instance, the left side of a picture at (row,col) must be compatible with the right side of the picture at (row,col-1). So, the problem must be solved in a given order so that the constraints can be propagated from one sub-picture to the other.
For some tiles, the sub-optimal solution can be very good from an artistic point of view (the dark tiles below are working well). For other tiles (the smith tiles in the notebook) either the sub-optimal problem cannot always be solved (because the constraints coming from the previous pictures can't be satisfied) or the sub-optimal problem will look bad from time to time.
So this idea of using sub-picture is really dependent on the kind of tiles used. You need to experiment. But it is art after all.
Example of use
First, we get an example picture:
srcImage = ImageCrop[ExampleData[{"TestImage", "Girl3"}], {190, 270}]
The picture is resized, converted to RGB and any alpha channel removed.
imgToAnalyze =
ImageResize[
ImageAdjust[
RemoveAlphaChannel[ColorConvert[srcImage, "RGB"], Black]], {50,
Automatic}]
For the dark tiles (knots), we decide to only use gray levels. First color is the background of the tiles. Other colors are for the circles and vertical and horizontal bands.
tileData =
mkDarkTiles[RGBColor[
0.5, 0.5, 0.5], {RGBColor[0., 0., 0.], RGBColor[1., 1., 1.]}];
It gives a total of 16 tiles. The more tiles, the more difficult it is to solve the problem. 16 is ok on my old computer.
tileData["allTilesImg"] // Length
The problem is solved on 15x15 sub pictures.
solution = partitionSolve[tileData, imgToAnalyze, 15];
The final picture is generated from the tiles and the solution.
img = createPict[tileData, solution];
And you'll get:

Have fun ! I hope the vectorial code will not have to be tuned to generate the tile pictures (rounding errors).
The notebook is attached to the post.
 Attachments:
Attachments: