Hello, I am not exactly sure what you mean by r in this case, or if you are integrating in a ball centered at {xp,yp,zp}.
However,
gauss = (1/4)*1/Sqrt[Pi]*
Exp[-((xp - x)^2 + (yp - y)^2 + (zp - z)^2)] + (3/4)*(1/Sqrt[Pi])*
Exp[-4*(Sqrt[(xp - x)^2 + (yp - y)^2 + (zp - z)^2] - 7/2)^2]
But, I am supposing now you are going to integrate in a ball centered at {xp,yp,zp}, so we can just move the ball to the origin:
gauss = Simplify[gauss /. {xp -> 0, yp -> 0, zp -> 0}]
Integrate doesn't give up, but I didn't wait for it to finish; so I gave it a little help:
gauss = Simplify[gauss /. x^2 -> r^2 - y^2 - z^2,
Assumptions :> r > 0]
This integrates quickly:
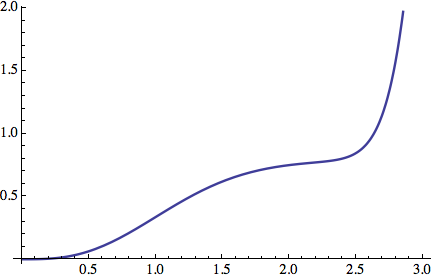
int = Integrate[4 Pi r^2 gauss, {r, 0, rBall}]
Plot[int, {rBall, 0, 3}]