Cool!. I like the disappearing effect. Simpler version with no disappearing

DynamicModule[{nPaths, nSteps, randomPaths, colors, color},
 nPaths = 10;
 nSteps = 125;
 SeedRandom[123];
 randomPaths = 
  Table[(RandomInteger[{0, 1}, {nSteps, 3}] - 1/2) 2, nPaths] // Map[AnglePath3D];
 colors = ColorData[112, "ColorList"];
 color[n_] := colors[[Max[Mod[n, Length@colors], 1]]];
 Manipulate[
  Graphics3D[
   MapIndexed[({color@First@#2, Line[#1[[1 ;; ns]]]} &), randomPaths],
    ViewPoint -> {5, 6, 3}, Boxed -> True, BoxStyle -> Opacity[.25], 
   PlotRange -> {{-15, 15}, {-15, 15}, {-15, 15}}], {ns, 2, nSteps, 1,
    AnimationRate -> 10, AnimationRepetitions -> 1, 
   AnimationRunning -> True, Appearance -> "Open"}]]

This works great, Rohit. Thanks again. I'm still looking for a couple of solutions. If you know where I can find them, please reply. The two improvements I'm trying to make are,...

1. Lock the scale of the box so that comparison is possible. As you see from the slider in my code. I'm trying to illustrate the change that occurs as the number of steps changes. But the automatic scaling in Mathematica defeats that.

2. I think it might be possible for the graphic to change as a fluid picture when the slider moves. The notebook pasted below requires the graphic to be recalculated from the keyboard after every change of the slider.

Yes, that helps, Henrik. Thanks. I don't know why but ListInterpolation[] never crossed my browser when I was considering the functions that almost did what I wanted. I'll get back to this thread after I've had a chance to try this out later today.

Jay,

my suggestion for this (if I understand your question correctly) would be using interpolation of these points - and here in particular ListInterpolation, because then you can set identical parametric limits on all line segments (here e.g. {0, 1}). My simple code (I do assume you have access to the documentation ...):

(* choosing 3 random vectors: *)

pts = RandomInteger[{-10, 10}, {3, 3}];
(* creating InterpolatingFunctions for each component; when you have \
only 3 points you can at most use 2 for 'InterpolationOrder: *)

ipLine = ListInterpolation[#, {0, 1}, InterpolationOrder -> 2] & /@ Transpose[pts];
(* showing the result - together with the original points: *)
Show[ParametricPlot3D[Through[ipLine[t]], {t, 0, 1}], Graphics3D[{Red, PointSize[Large], Point[pts]}]]

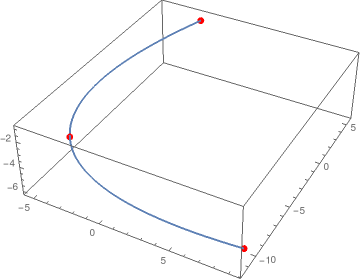
When doing this for more sets of points it makes sense defining a function, e.g.:

lineFunc[t_][pts_List] := Module[{func3},
  func3 = ListInterpolation[#, {0, 1}, InterpolationOrder -> 2] & /@ Transpose[pts];
  Through[func3[t]]
  ]

and using this function:

(* e.g. creating 4 sets of 3 points: *)
{pts1, pts2, pts3, pts4} = Partition[RandomInteger[{-10, 10}, {12, 3}], 3];
(* and showing the result:  *)
ParametricPlot3D[Evaluate[lineFunc[t] /@ {pts1, pts2, pts3, pts4}], {t, 0, 1}]

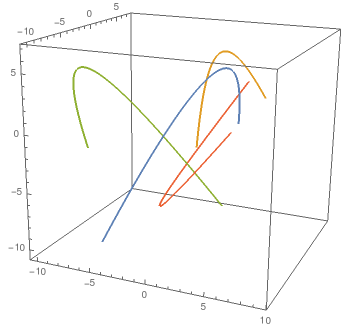
Does that help? Regards -- Henrik