Many thanks for your advice. My purpose is to define the PDF of the difference of two gaussian random variables (X and Y) if X-Y<0 and see the mean and variance. At this stage I just really want to learn how to define a custom PDF and ask for the mean and variance.

pdfx[x_] = 
 ConditionalExpression[
  PDF[(1/Sqrt[2*Pi]*\[Sigma]1) *(E^-1/
       2*((x - \[Mu]1)/\[Sigma]1)^2), {x, -Infinity, 
    Infinity}], \[Sigma]1 > 0]

Mean[pdfx]

and

Variance[pdfx]

distXminusY = TransformedDistribution[x - y,
  {x \[Distributed] NormalDistribution[\[Mu]1, \[Sigma]1], 
   y \[Distributed] NormalDistribution[\[Mu]2, \[Sigma]2]}]
distCensored = CensoredDistribution[{-Infinity, 0}, distXminusY]
Mean[distCensored] // FullSimplify
(* -((E^(-((\[Mu]1 - \[Mu]2)^2/(2 (\[Sigma]1^2 + \[Sigma]2^2))))
    Sqrt[\[Sigma]1^2 + \[Sigma]2^2])/Sqrt[2 \[Pi]]) + 
 1/2 (\[Mu]1 - \[Mu]2) Erfc[(\[Mu]1 - \[Mu]2)/(
   Sqrt[2] Sqrt[\[Sigma]1^2 + \[Sigma]2^2])] *)
Variance[distCensored]
(* a long output - maybe can be simplified by assuming \[mu]1 <= \[mu]2  *)

Yes, this assumptation can be made: Assumptions -> [Mu]1 <= [Mu]2 as well as [Sigma]1==[Sigma]2.

Would you mind having a look at my notebook?

distXminusY = 
 Assuming[\[Sigma] > 0, 
  TransformedDistribution[
   x - y, {x \[Distributed] NormalDistribution[\[Mu]1, \[Sigma]], 
    y \[Distributed] NormalDistribution[\[Mu]2, \[Sigma]]}]]

distCensored = CensoredDistribution[{-Infinity, 0}, distXminusY]

MeanOfdistCensored = 
 Simplify[Assuming[\[Mu]1 <= \[Mu]2, Mean[distCensored]]]

Assuming[\[Mu]1 <= \[Mu]2, PDF[distCensored, z]]

Thanks for your help, I'm really grateful!

Attila

@Attila Horvath Are you aware of Conditioned?

With it, you can compute conditional probability, conditional expectation (and through the workaround/definition also conditional variance). I tested these computations with the example and problem sets from US textbooks and they work just fine. When i looked at those texts i did notice the term "conditional distribution" but i have not read up on it; i am pre-"Introduction to Probability", hehe. It may or may not be possible to define a conditional distribution with that function, i am just wondering if you were aware of the nice function. Afaik MAPLE does not have it.

The direct approach would be to try to determine the cdf of x1 conditional on x1 > x2:

cdf = Probability[x1 <= x0 \[Conditioned] x1 > x2,
  {x1 \[Distributed] NormalDistribution[mu1, sigma1],
   x2 \[Distributed] NormalDistribution[mu2, sigma2]},
  Assumptions -> {mu1 <= mu2, sigma1 > 0, sigma2 > 0}]

But this just returns the command. This is either because Probability doesn't know how to obtain the answer or because there is no closed-form answer. So more basic approaches are needed.

We first determine the joint pdf of x1 and x2 given that x1 > x2 and then integrate over x2 to get the pdf of x1 conditional on x1 > x2.

(* Probability that x1 > x2 *)
p = Probability[x1 > x2,
  {x1 \[Distributed] NormalDistribution[mu1, sigma1],
   x2 \[Distributed] NormalDistribution[mu2, sigma2]},
  Assumptions -> {sigma1 > 0, sigma2 > 0}]
(* 1/2 Erfc[(mu1 - mu2)/(Sqrt[2] Sqrt[sigma1^2 + sigma2^2])] *)

(* Joint distribution of x1 and x2 given that x1 > x2 *)
jointPDF = Piecewise[{{PDF[NormalDistribution[mu1, sigma1], x1]*
     PDF[NormalDistribution[mu2, sigma2], x2]/p, x1 > x2}}, 0]

(* Integrate over x2 to get marginal pdf for x1 given that x1 > x2 *)
pdfx1 = Integrate[jointPDF, {x2, -Infinity, x1},
  Assumptions -> {x1 \[Element] Reals, mu1 <= mu2, sigma1 > 0, 
    sigma2 > 0}]
(* (E^(-((mu1 - x1)^2/(2 sigma1^2)))*
  Erfc[(mu2 - x1)/(Sqrt[2] sigma2)])/(Sqrt[2 \[Pi]] sigma1 Erfc[(-mu1 + mu2)/(Sqrt[2] Sqrt[sigma1^2 + sigma2^2])]) *)

There doesn't appear to be a nice closed form for the cdf, mean, or variance.

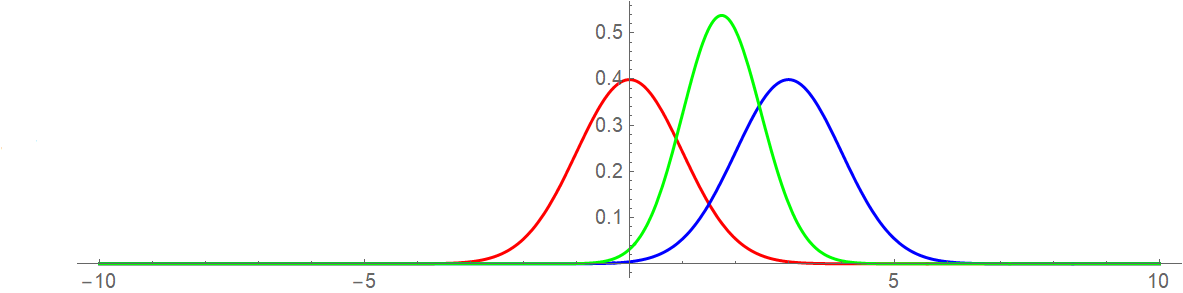
This does appear to match what you got from R:

parms = {mu1 -> 0, mu2 -> 3, sigma1 -> 1, sigma2 -> 1};
Plot[{PDF[NormalDistribution[mu1, sigma1] /. parms, x1],
  PDF[NormalDistribution[mu2, sigma2] /. parms, x1],
  pdfx1 /. parms}, {x1, -10, 10},
 PlotStyle -> {Red, Blue, Green}, PlotRange -> All, AspectRatio -> 1/4]

Yes, that is how to get the marginal distribution of x2 given that x1 > x2.

But I would avoid the statement "X2 distribution restricts everything" because one could just as easily (and incorrectly) state that the "X1 distribution restricts everything" as one could rephrase your other statement as "x2 can't go further as it bumps into x1." I would say that such a "cause-and-effect" statement is both wrong and unnecessary.