I used Mathematica to create the following puzzle. A playable version is here. Normal sudoku rules apply. Digits cannot repeat along diagonals except when they appear on an arrow. In which case, they must repeat but only in the cell indicated by the arrow and digit (ie giving the direction and distance of the repeated cell). All of the numbers 1 to 8 must appear on (at least) one arrow. 
This was selected by Youtube channel Cracking the Cryptic.

One of the top comments: 
I just asked Mathematica to come up with it for me, and blam, there it was.
So, first a few functions.
sudokucheck[perm_] := With[{p = Transpose[{Range[9], perm}]}, Length[Union[Ceiling[p/3]]] == 9];
diagcheckline[perm_] := Module[{p, bad},
p = Transpose[{Range[Length[perm]], perm}];
Select[#, Length[#] > 1 &] & /@ {GatherBy[p, #[[1]] - #[[2]] &], (GatherBy[p, #[[1]] + #[[2]] &])}];
diagdist[perm_] := Sort[Abs[#[[1, 1]] - #[[2, 1]]] & /@ Flatten[Subsets[#, {2}] & /@ Flatten[diagcheckline[perm], 1], 1]]
A set of values in a sudoku can be considered a permutation. We can find all the permutations that would pass the boxes test. Then we can find all the permutations that would satisfy a queen's position, and then find all 7 cliques. FindClique[queengraph, {8}, All] reveals that no 8-cliques exist.
pp = Permutations[Range[9]];
pass = Select[pp, sudokucheck[#] &];
queenprep = Select[pass, Length[Union[diagdist[#]]] == 0 &];
gatherqueen = Sort[GatherBy[queenprep, canonicalpermutation]];
canonqueen = First /@ gatherqueen;
queen = Join[canonqueen, Flatten[Drop[#, 1] & /@ gatherqueen, 1]];
queengraph = Graph[UndirectedEdge @@@ Select[Subsets[Range[144], {2}], Count[Differences[queen[[#]]][[1]], 0] == 0 &]];
queencliques = First /@ GatherBy[Sort[Sort /@ FindClique[queengraph, {7}, All]], Sort[Position[gatherqueen, #][[1, 1]] & /@ queen[[#]]] &];
There are four basic ways to make a 7-clique with queens:
Row[Graphics[{EdgeForm[{Black}],White,Rectangle/@Tuples[Range[9],{2}],Table[{Hue[k/7],Rectangle/@Transpose[{queen[[#[[k]]]],Range[9]}]},{k,1,7}], Thickness[.015],Black,Table[{Line[{{k,1},{k,10}}],Line[{{1,k},{10,k}}]},{k,1,10,3}]},ImageSize->250]&/@queencliques]

There are 19 basic ways to avoid diagonals.
Grid[Partition[Graphics[{EdgeForm[Black],White,Rectangle/@Tuples[Range[9],{2}],LightGray,Rectangle/@Select[Tuples[Range[9],{2}],EvenQ[Total[#]]&],Black,Rectangle/@Transpose[{#,Range[9]}]},ImageSize->90]&/@canonqueen,UpTo[10]]]

That's as far as I got for awhile. I don't recall making any good sudoku puzzles from the 7-cliques, though there may be a method I missed. I looked at the 6-cliques without anything amazing occuring to me. A few weeks ago I came back to the problem and pondered making a Super-X sudoku, where the 5 main diagonals each way would not have repeats. I don't think I found a solution. Then I tried reversing it -- what if all the repeats were just on a few diagonals. I found a position where only 4 diagonals had repeats, and created the following puzzle.
Diagonal duplicates appear only in the marked diagonals. In the DUPE column, the numbers that duplicate are shown. In the MISS column, the digits that are missing from a diagonal are shown.
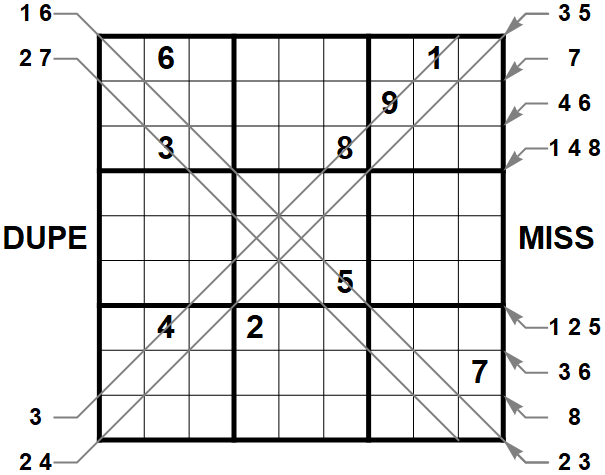
Not a terrible puzzle, but certainly not elegant. But it seemed there might be something. What could I call the puzzles of this type? Dupe .. Duplicate....
Duplicate Bridge! What if all the repeats were set up as bridges? A number on an arrow would give the distance and direction to the duplicate number. After a search, that led to the following puzzle.

That's more elegant. Unfortunately, when restricted to just one duplication per number, there were only three basic configurations to choose from. Two of them were used in the puzzle immediately above. Then it occured to me that I could allow more than a single 1-bridge. A 9-bridge would be impossible, but there could be solutions with an 8-bridge and all smaller.
If I could find a configuration that had 1 to 8 bridges, then a puzzle with no givens might be possible. If any were missed, say 8, then there would be no way to distinguish 8 and 9 on the grid without some extra information being given.
So, create all the valid sudoku permutations that have 1, 2, 3, ..., 8 bridges, and then put the canonical queen positions at the end for the 9's.
glass = Select[pass, Length[Union[diagdist[#]]] == 1 &];
glaze = Join[SplitBy[SortBy[glass, {Union[diagdist[#]], -Length[diagdist[#]]} &], Union[diagdist[#]] &], {canonqueen}];
Length /@ glaze
{656, 1032, 224, 536, 400, 80, 48, 8, 19}
The 6 to 9 configs are highly restricted, so lets find all that might work.
part69=Select[Union[Tuples[Take[glaze,-4]]],
Count[#[[1]]-#[[2]],0]==0&&Count[#[[1]]-#[[3]],0]==0&&Count[#[[2]]-#[[3]],0]==0&&
Count[#[[1]]-#[[4]],0]==0&&Count[#[[2]]-#[[4]],0]==0&&Count[#[[3]]-#[[4]],0]==0&];
There are 2819 possibilities. So now, we find all the full configurations that might work.
first5big = Take[glaze, 5];
pass69=Monitor[Table[
case1=(Select[#,Count[#-part69[[n,1]],0]==0&&Count[#-part69[[n,2]],0]==0&&Count[#-part69[[n,3]],0]==0&&Count[#-part69[[n,4]],0]==0&]&/@first5big);
If[Min[Length/@case1]>0,
tt=Select[Tuples[case1],Max[Count[#[[1]]-#[[2]],0]&/@ Subsets[#,{2}]]==0&];
Join[#,part69[[n]]]&/@tt,Sequence@@{}],{n,1,Length[part69]}],n];
Running the code, it turns out there there is only a single configuration that works! It's unique. So from there, it then needs to be set up as a puzzle, and hopefully it's human solvable. We have a computer solvable puzzle already. It's unique! Go find it, computer. But that's not a fun solving experience for a human.
There are 2^12 = 4096 ways the arrows could be set up, so I decided to go for an easy arrow configuration to see if I could solve it. After a few tweaks I came up with a configuration that had a fairly good set of solving logic. Done!
Many thanks to Philipp Blume for help, and to Cracking the Cryptic and Siman Anthony for accepting it.
 Attachments:
Attachments: